chap 10 - 降维与度量学习

10.1 k近邻学习(k-Nearest Neighbor, kNN)

类型：监督学习

工作机制： 给定测试样本，基于某种距离度量计算出训练集中与该样本距离最近的k个训练样本，然后基于这k个“邻居”的信息来进行预测。通常，在分类任务中采取“投票法”，回归任务中采取“平均法”，还可基于距离的远近使用“加权投票法”或“加权平均法”。

特点：

• 懒惰学习(lazy learning)的著名代表。此类学习技术在训练阶段仅仅保存训练样本，训练时间开销为零，待收到测试样本之后再处理。
• 之前的算法都是“急切学习”(eager learning)算法，即收到训练样本就马上处理。

kNN的关键：

• k取值不同，分类结果会显著不同；
• 距离度量的计算方式会导致同一测试样本有不同的“近邻”。

举一个例子🌰：

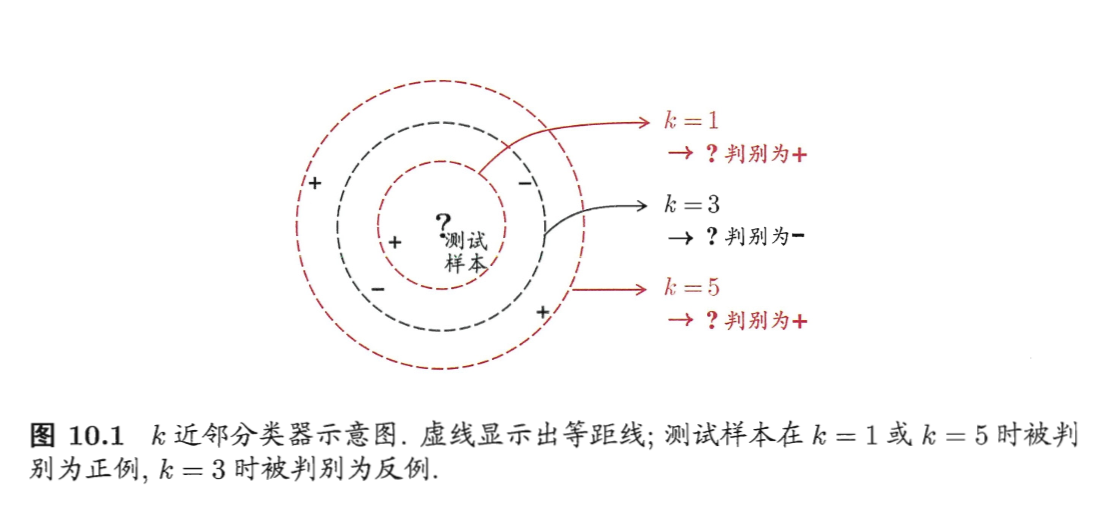
分类性能：

假设距离计算是“恰当”（能恰当找到$k$个近邻）的，取$k=1$，讨论“最近邻分类器”($1NN, k=1$)在二分类问题上的性能。

给定测试样本$x$，若其最近邻样本为$z$，则最近邻分类器出错的概率就是$x$与$z$类别标记不同的概率，即

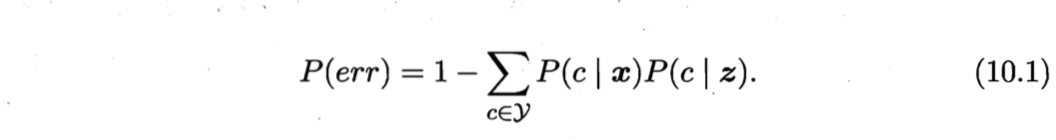
假设样本i.i.d.，且对任意$x$和任意小正数$δ$，在$x$的$δ$邻域内总能找到一个训练样本；换言之，对任意测试样本，总能在任意近的范围内找到式(10.1)中的训练样本$z$。

即假设训练样本密度足够大，或称为“密度采样”(dense sample)。

令$c^\ast = \arg \max_{c \in \cal{Y}} P(c \,|\, \boldsymbol{x})$表示贝叶斯最优分类器的结果，有 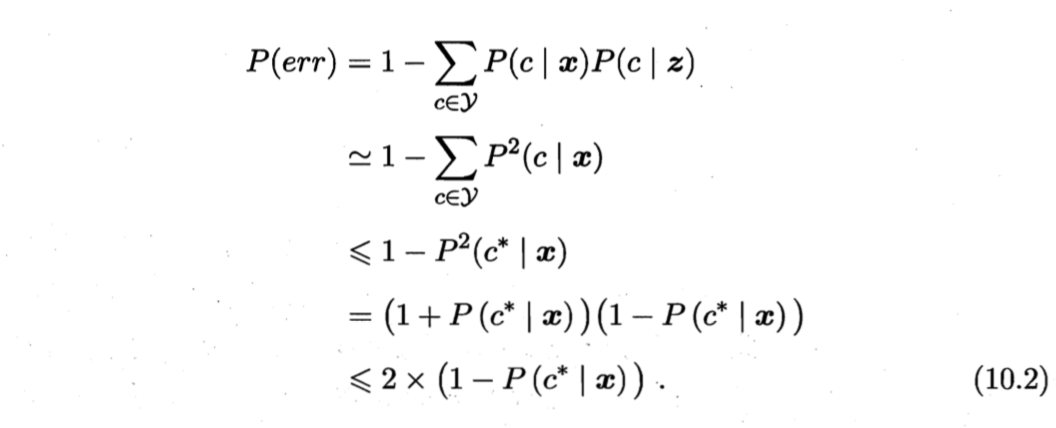可以看出，1NN虽然简单，但其泛化错误率不超过贝叶斯最优分类器错误率的两倍。 【严格分析参阅[Cover and Hart, 1967]】

10.2 低维嵌入

维数灾难

kNN的缺陷：“密度采样”难以满足。

1. 属性维数越多，要满足密度采样条件的样本数目是无法达到的； 如，取$δ=0.001$，仅考虑单个属性，则需$1000$个样本点平均分布在归一化后的属性取值范围内；若属性维数为$20$，则至少需$(10^3)^{20}=10^{60}$个样本。【作为参照：宇宙间基本粒子的总数约为$10^{80}$（一粒灰尘中含有几十亿个基本粒子）】
2. 在高维空间计算距离十分困难。

如，当维数很高时计算内积都十分困难。

以上在高维情形下出现的数据样本稀疏、距离计算困难等问题，是所有机器学习方法共同面临的严重障碍，被称为“维数灾难”(curse of dimensionality).

[Bellman, 1957]最早提出，亦称“维数诅咒”、“维数危机”。

如何缓解维数灾难

• 特征选择（chap 11）
• 降维（dimension reduction）/ 维数约简：通过某种数学变换将原始高维属性空间转变为一个低维“子空间”(subspace)。在子空间内，样本密度大幅提高，距离计算变得简单。

可以降维的原因：

虽观测到的样本数据是高维的，但很多时候，与学习任务密切相关的也许仅仅是某个低维分布，即高维空间中的一个低维“嵌入”(embedding)。图10.2给出了一个例子。原始高维空间中的样本点，在低维嵌入子空间中更容易学习。

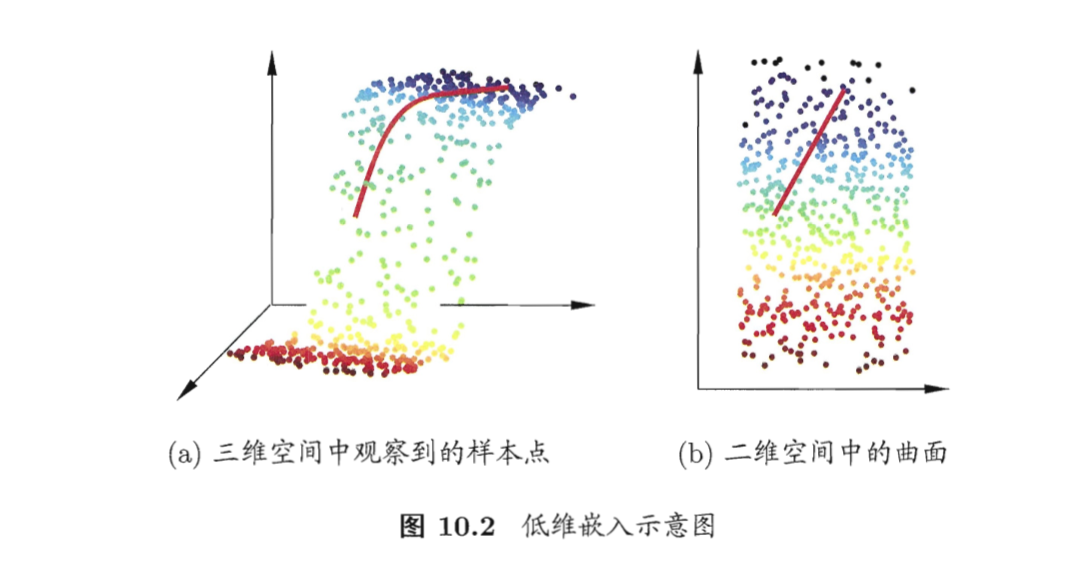
多维缩放 (Multiple Dimensional Scaling, MDS)

特点：在低维空间中保持了原始空间中样本之间的距离。

推导：

符号&假设：

• $\boldsymbol{D} \in \mathbb{R}^{m \times m}$：$m$个样本在原始空间的距离矩阵，其第$i$行$j$列的元素$dist_{ij}$为样本$x_i$到$x_j$的距离；
• $\boldsymbol{Z} \in \mathbb{R}^{d’ \times m}$：样本在$d’$维空间的表示，$d’≤d$，且任意两个样本在$d’$维空间中的欧式距离等于原始空间中的距离，即$||z_i - zj|| = dist{ij}$。

目标：求Z

① 求内积矩阵$B=Z^T Z$

令$B=Z^T Z \in \mathbb{R}^{m \times m}$，其中$B$为降维后样本的内积矩阵，$b_{ij} = z_i^T z_j$，有

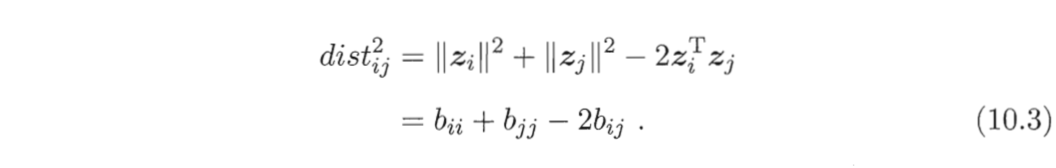
为了便于讨论，令降维后的样本$Z$被中心化，即$\sum_{i=1}^m zi=0$。显然，矩阵B的行与列之和均为零，即$\sum{i=1}^m b{ij} = \sum{j=1}^m b_{ij} = 0$。易知，

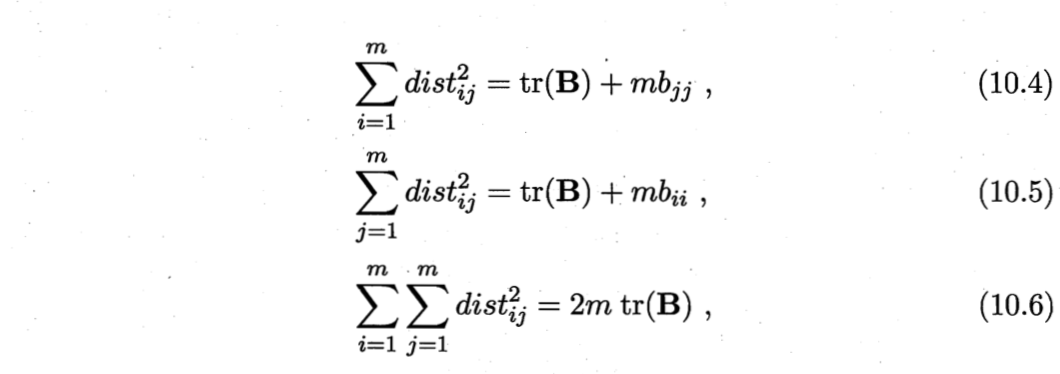
其中，tr(·)表示矩阵的迹(trace)，$tr(B) = \sum_{i=1}^m ||z_i||^2 $。令

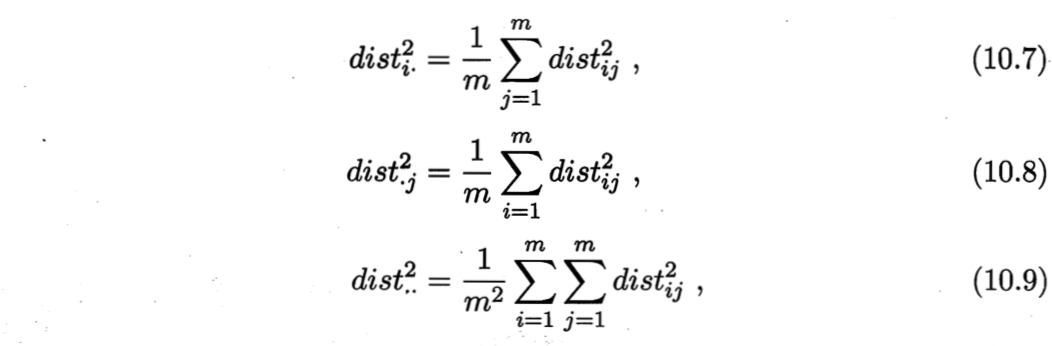
由式(10.3)和式(10.4)~(10.9)可得

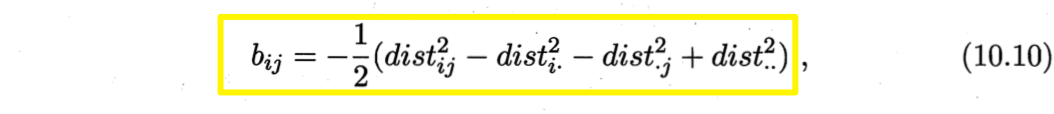
由此，即可通过降维前后保持不变的距离矩阵D求取内积矩阵B。

②通过内积矩阵B求Z

对矩阵B做特征值分解(eigenvalue decomposition)，$B=V \Lambda V^T$，其中$\Lambda=diag(\lambda_1,\lambda_2,\cdots, \lambda_d)$为特征值构成的对角矩阵，$\lambda_1 ≥ \lambda_2≥\cdots ≥\lambda_d$，$V$为特征向量矩阵。

假定其中有$d^\ast$个非零特征值，它们构成对角矩阵$\Lambda_\ast=diag(\lambda_1,\lambda2,\cdots, \lambda{d^\ast})$，令$V_\ast$表表示相应的特征向量矩阵，则$Z$可表达为

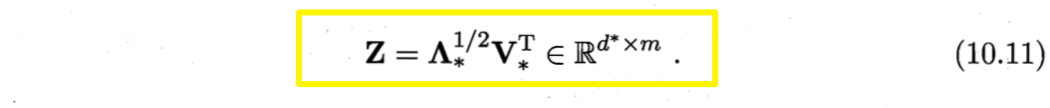
现实应用中为了有效降维，往往仅需降维后的距离与原始空间中的距离尽可能接近，不必严格相等。此时，可取$d’<<d$个最大特征值构成对角矩阵$\tilde{\Lambda}=diag(\lambda_1,\lambda2,\cdots,\lambda{d’})$，令 $\tilde{V}$表示特征向量矩阵，则$Z$可表达为

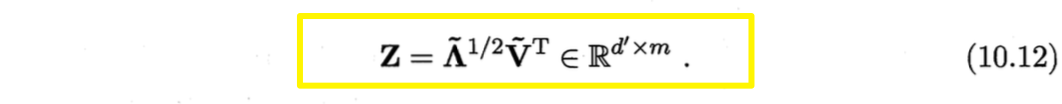
算法描述：

其他方法：

最简单：线性降维，对原始高维空间进行线性变换。

给定$d$维空间中的样本$X=(x_1,x_2, \cdots, x_m) \in \mathbb{R}^{d \times m}$，变换后得到$d’≤d$维空间中的样本

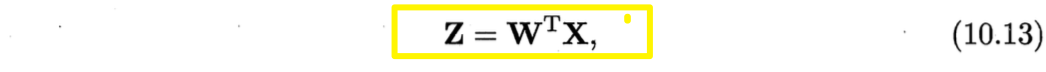
符号：

• $\boldsymbol{W} \in \mathbb{R}^{d \times d’}$：变换矩阵；
• $\boldsymbol{Z} \in \mathbb{R}^{d’ \times m}$：样本在新空间中的表达。

变换矩阵W可视为$d’$个$d$维向量，是第$i$个样本与这$d’$个基向量分别做内积而得到的$d’$维属性向量。换言之，$\boldsymbol{z}_i$是原属性向量$\boldsymbol{x}_i$在新坐标系${w_1,w2, \cdots, w{d’}}$中的坐标向量。若$\boldsymbol{w}_i$与$\boldsymbol{w}_j (i \neq j)$正交，则新坐标系是一个正交坐标系，此时$\boldsymbol{W}$为正交变换。显然，新空间中的属性是原空间中属性的线性组合。

关键：W

对W施加不同的约束相当于对低维子空间有不同的要求。

降维效果评估：

通常，比较降维前后学习器的性能，若性能有所提高，则认为降维起到的作用。若将维数降至二维或三维，则可通过可视化技术直观判断。

10.3 主成分分析 (Principal Component Analysis, PCA)

思路：

对正交属性空间中的样本点，如何寻找一个超平面（直线的高维推广）恰当描述所有样本？

超平面应满足的性质：

• 最近重构性：样本点到这个超平面的而距离都足够近；
• 最大可分性：样本点在这个超平面上的投影能尽可能分开。

PCA的最近重构性推导：

符号&假设：

• $\sum_i \boldsymbol{x}_i =0$：假定对数据样本中心化；
• ${w_1,w_2, \cdots, w_d}$：投影变换后的新坐标系，$\boldsymbol{w}_i$为标准正交基向量，$||\boldsymbol{w}_i||_2 =1, \boldsymbol{w}_i^T \boldsymbol{w}_j=0 (i \neq j)$；
• $\boldsymbol{z}i=(z{i1};z{i2};\cdots;z{id’})$：样本点$\boldsymbol{x}i$在低维坐标系中的投影（丢弃新坐标系中的部分坐标，将维度降低至$d’<d$），$\boldsymbol{z}{ij} = \boldsymbol{w}_j^T \boldsymbol{x}_i $是$\boldsymbol{x}_i$在低维坐标系下第$j$维的坐标。
• $\hat{\boldsymbol{x}}i = \sum{j=1}^{d’} z_{ij} \boldsymbol{w}_j$：基于$\boldsymbol{z}_i$重构$\boldsymbol{x}_i$得到的$\boldsymbol{x}_i$坐标。

考虑整个训练集，原样本点$\boldsymbol{x}_i$与基于投影重构的样本点$\hat{\boldsymbol{x}}_i$之间的距离为

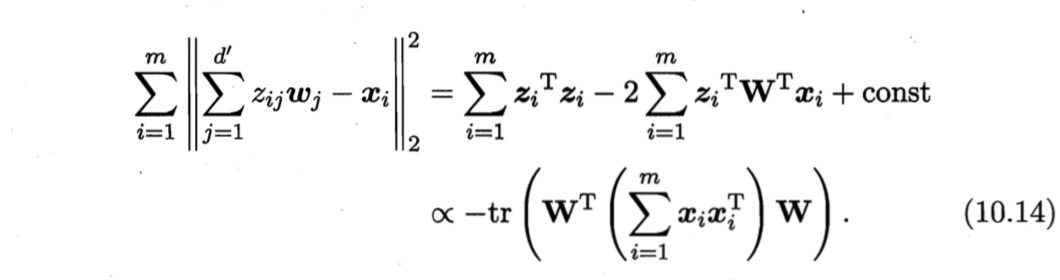
正交矩阵性质$A^TA=I, \, A^{-1}=A^T$.

其中,$\boldsymbol{W} = (\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots,\boldsymbol{w}_d)$。根据重构性，应最小化式(10.14)。考虑到$\boldsymbol{w}_i$标准正交基，$\sum_i \boldsymbol{x}_i \boldsymbol{x}_i^T$是协方差矩阵，有

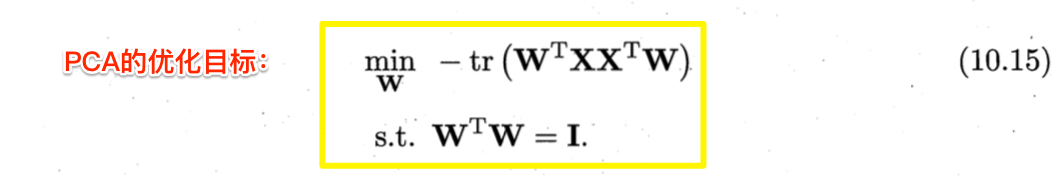
严格来说, 协方差矩阵是$\frac{1}{m-1} \sum_{i=1}^m \boldsymbol{x}_i \boldsymbol{x}_i^T$, 但前面的常数项在此不发生影响。

PCA的最大可分性推导：

符号&假设：

• $\boldsymbol{W}^T \boldsymbol{x}_i$：样本点$\boldsymbol{x}_i$在新空间中超平面上的投影；
• $\sum_i \boldsymbol{W}^T \boldsymbol{x}_i \boldsymbol{x}_i^T \boldsymbol{W}$：投影后样本点的方差。

目标：投影后样本点方差最大化，如图10.4。

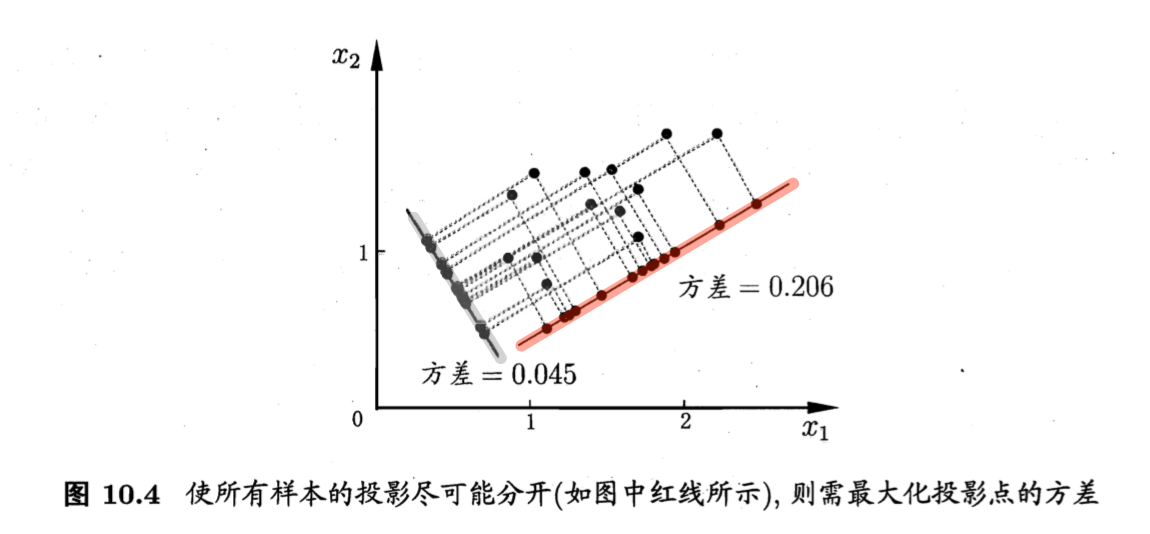
优化目标：

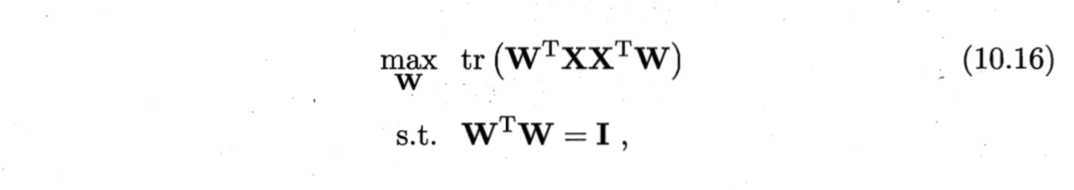
目标函数求解：

(10.15)与(10.16)等价，用拉格朗日乘子法可得

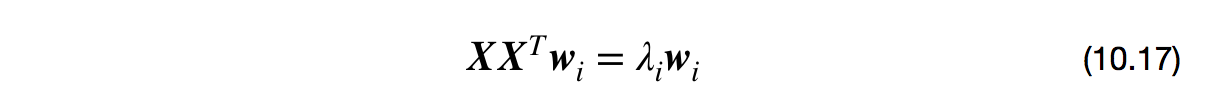
求解方法：

对协方差矩阵$\boldsymbol{X} \boldsymbol{X}^T$进行特征值分解，将求得的特征值排序$\lambda_1 ≥ \lambda_2≥\cdots ≥\lambda_d$，取前$d’$个特征值对应的特征向量构成$\boldsymbol{W} = (\boldsymbol{w}_1,\boldsymbol{w}2,\cdots,\boldsymbol{w}{d’})$，即为PCA的解。

算法描述：

低维空间维数d’的确定：

1. 用户指定d’；
2. 在d’不同的低维空间里训练开销较小的学习器（如，kNN），用CV选择较好的d’值。
3. 设置重构阈值，如t=95%，再选取使式(10.18)成立的最小d’。

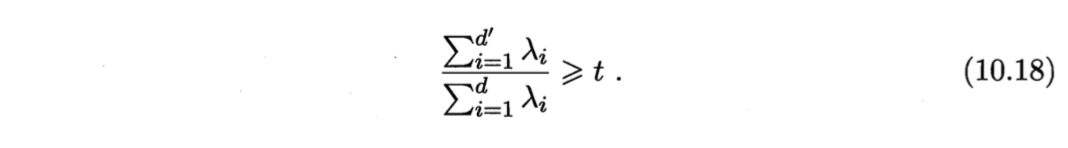
投影新样本到低维空间： 保留W与样本均值向量即可。

舍弃d-d’个特征值的作用：

1. 使样本采样密度增大；
2. 当数据受到噪声影响时，最小特征值所对应的特征向量往往与噪声有关，将它们舍弃能在一定程度上起到去噪的效果。

10.4 核化(kernelized)线性降维

PCA是一种线性降维方法，但现实中很多时候需要非线性映射才能找到合适的低维嵌入。如图10.6所示。

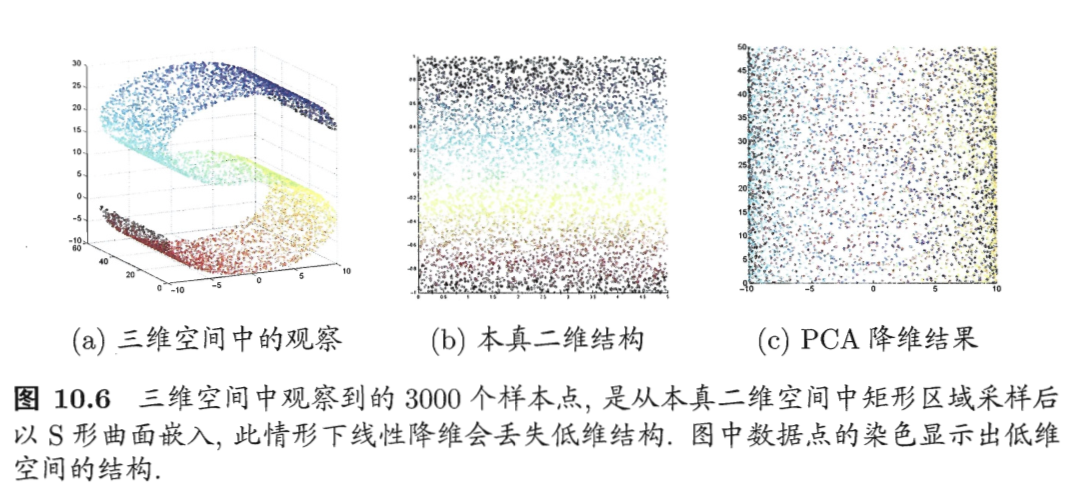
为了和降维后的结果加以区分，称“原本采样的”低维结构为“本真”(intrinsic)低维空间。

核主成分分析(Kernelized PCA, KPCA)

• 非线性降维方法
• [Schölkopf et al., 1998]

推导

符号：

• $\boldsymbol{W} = (\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots,\boldsymbol{w}_d)$：低维超平面；
• $\boldsymbol{x}_i$：原始空间样本点；
• $\boldsymbol{z}_i$：把$\boldsymbol{x}_i$投影到低维平面后的像；
• $\phi$：把$\boldsymbol{x}_i$投影为$\boldsymbol{z}_i$的映射，$\boldsymbol{z}_i = \phi(\boldsymbol{x}_i), \, i=1,2,\cdots, m$；
• $\boldsymbol{K}$：核函数$k$对应的核矩阵；

假定我们将在高维特征空间中把数据投影到由$\boldsymbol{W} = (\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots,\boldsymbol{w}_d)$确定的超平面上，则对于$\boldsymbol{w}_i$，由式(10.17)有

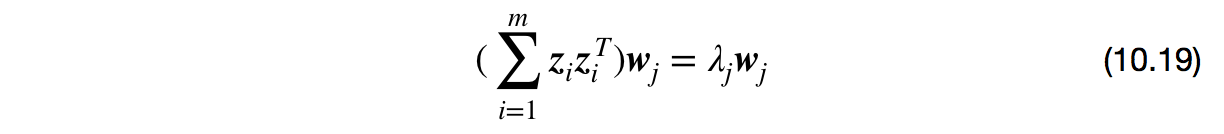
其中，$\boldsymbol{z}_i$是样本点$\boldsymbol{x}_i$在高维特征空间中的像。易知 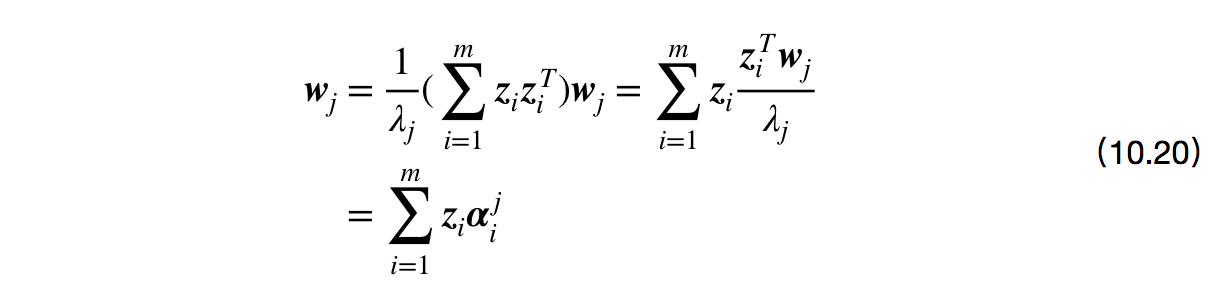其中，$\boldsymbol{\alpha}_i = \frac{1}{\lambda_j} \boldsymbol{z}_i^T \boldsymbol{w}_j$是$\boldsymbol{\alpha}_i$的第$j$个分量，假定$boldsymbol{z}_i$是由原始属性空间中样本点$\boldsymbol{x}_i$通过映射$\phi$产生，即$\boldsymbol{z}_i = \phi(\boldsymbol{x}_i), \, i=1,2,\cdots, m$

①若$\phi$能被显示表达，则先将样本映射至高维特征空间，再在特征空间中实施PCA即可。式(10.19)变换为

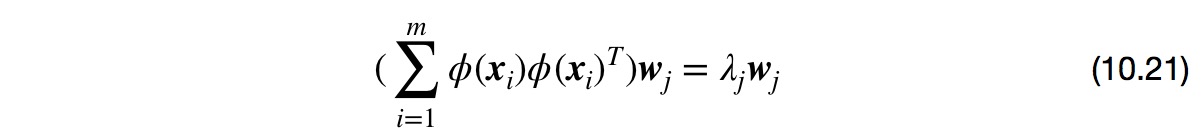
式(10.20)变换为

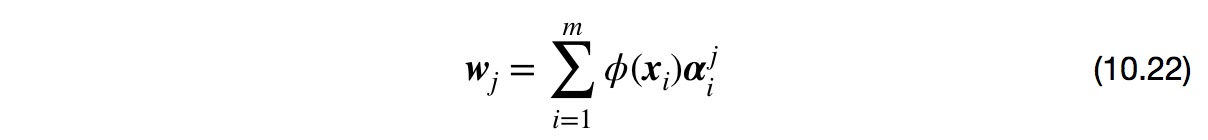
②大多数情况，不知道$\phi$的具体形式，引入核函数

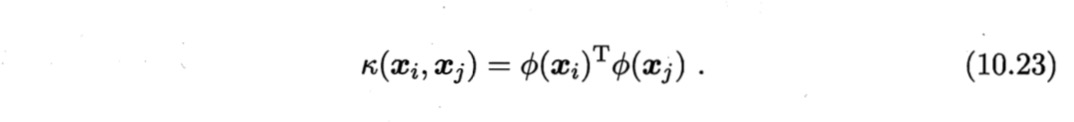
将式(10.22)和(10.23)代入(10.21)后化简可得

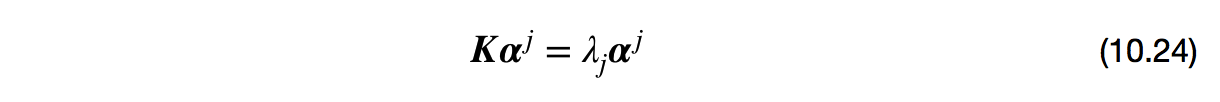
其中，$\boldsymbol{K}$为核函数$\kappa$对应的核矩阵，$\boldsymbol{K}_{ij} = \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j)$，$\boldsymbol{\alpha}^j = (\alpha^j_1, \alpha^j_2, \cdots, \alpha^j_m)$。用特征值分解求解式(10.24)，取$\boldsymbol{K}$最大的$d’$个特征值对应的特征向量即可。

对新样本$\boldsymbol{x}$，其投影后的第$j(j=1,2,…,d’)$维坐标为

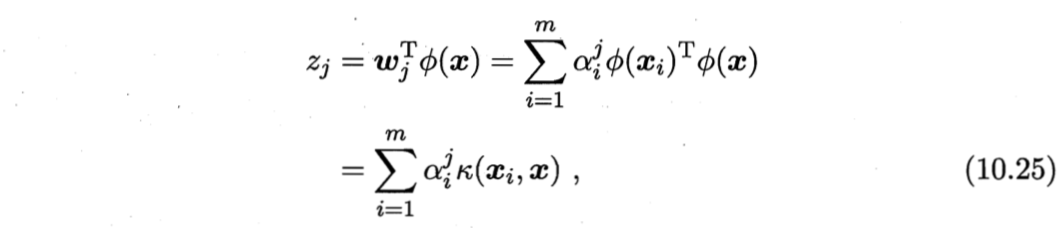
其中，$\boldsymbol{\alpha}^i$已经规范化。式(10.25)显示出，为获得投影后的坐标，KPCA需对所有样本求和，因此其计算开销较大。

10.5 流形学习 (manifold learning)

流形：是在局部与欧式空间同胚的空间，换言之，它在局部具有欧式空间的性质，能用欧氏距离来进行距离计算。

启发：

• 若低维流形嵌入到高维空间中，则数据样本在高维空间的分布虽然看上去十分复杂，但在局部上仍具有欧式空间的性质。因此，易在局部建立降维映射关系，然后再设法将局部映射关系推广到全局。
• 当维数被降至二维或三维时，能对数据进行可视化展示。

10.5.1 等度量映射(Isometric Mapping, Isomap) [Tenenbaum et al., 2000]

基本出发点：

认为低维流形嵌入到高维空间后，直接在高维空间中计算距离具有误导性，因为高维空间中的直线距离在低维嵌入流形中不可达。

举一个例子🌰：

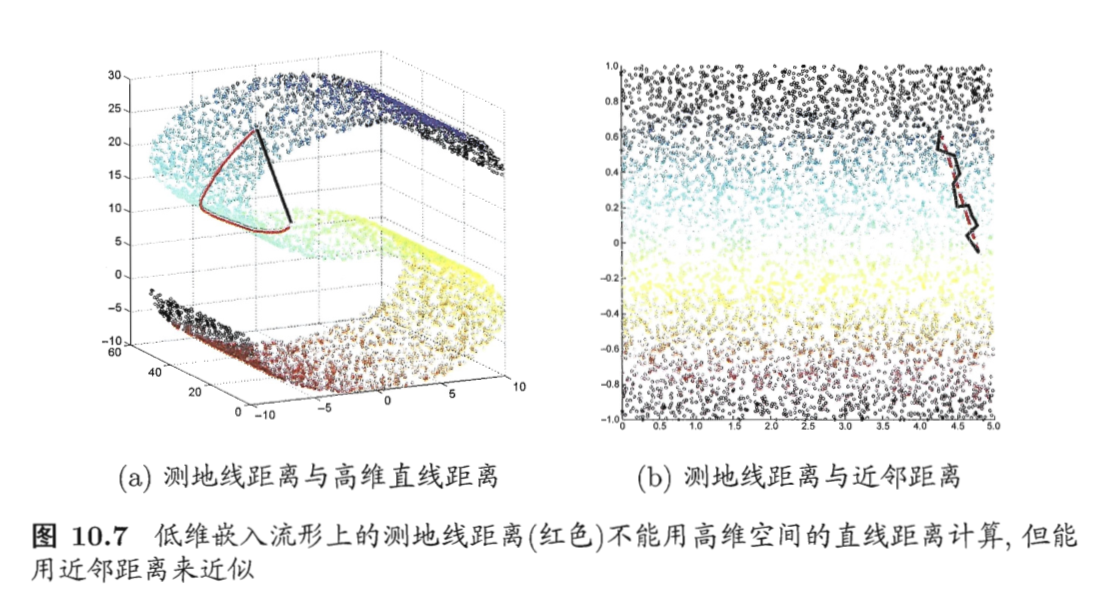
低维嵌入流形上两点间的距离是“测地线”(geodesic)距离：想象一只虫子从一点爬到另一点，如果它不能脱离曲面行走，那么图10.7(a)中的红色曲线是距离最短的路径，即S曲面上的测地线，测地线距离是两点之间的本真距离。显然，直接在高维空间中计算直线距离是不恰当的。

如何计算测地线距离

利用流形在局部上与欧式空间同胚的性质，对每个点基于欧式空间找出其近邻点，然后就能建立一个近邻连接图，图中近邻点之间存在连接，而非近邻点之间不存在连接，于是，计算两点之间测地线距离的问题，就转变为计算近邻连接图上两点之间的最短路径问题。从图10.7(b)可看出，基于近邻距离逼近能获得低维流形上测地线距离很好的近似。

如何在近邻连接图上计算两点间的最短路径

• 可采用著名的Dijkstra算法或Floyd算法；
• 得到任意两点的距离之后，通过10.2节介绍的MDS方法来获得样本在低维空间中的坐标。

1972年图灵奖得主E.W.Dijstra和1978年图灵奖得主R.floyd分别提出的著名算法，参阅数据结构教科书。

Isomap算法描述：

• 6：MDS参见10.2节。

如何将新样本映射到低维空间

*** 常用解决方案：回归**。将训练样本的高维空间坐标作为输入、低维空间坐标作为输出，训练一个回归学习器，然后对新样本的低维坐标进行预测。 * 权宜之计，目前似乎并没有更好的办法。

构建近邻图的两种常见做法

1. 指定近邻点个数k：如，选择欧式距离最近的k个点作为近邻点，这样得到的近邻图被称为“k近邻图”；
2. 指定距离阈值𝜖：距离小于𝜖的点被认为是近邻点，这样得到的近邻图被称为“𝜖近邻图”。

不足：

1. 短路：近邻范围过大，距离很远的点被误认为近邻；
2. 断路：近邻范围过小，图中有些区域与其他区域不存在连接。

都会给后续的最短路径计算造成误导。

10.5.2 局部线性嵌入(Locally Linear Embedding, LLE) [Roweis and Saul, 2000]

与Isomap的区别：

• Isomap试图保持近邻样本之间的距离；
• LLE试图保持邻域内样本之间的线性关系，如式(10.26)。

举一个例子🌰：

如图10.9，假设样本点$\boldsymbol{x}_i$的坐标能通过其邻域样本$\boldsymbol{x}_j$,$\boldsymbol{x}_k$,$\boldsymbol{x}_l$的坐标通过线性组合重构，即

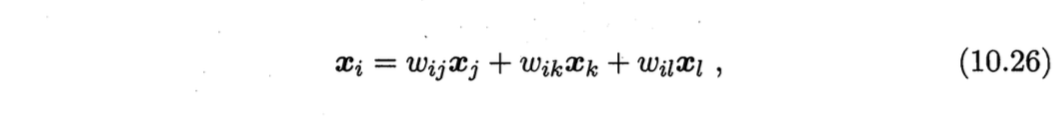
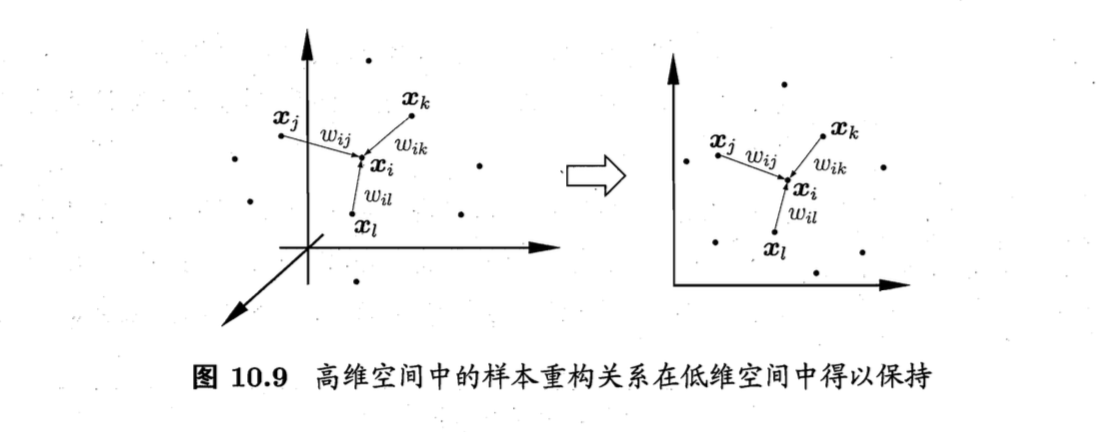
LLE的推导

确定线性组合系数$\boldsymbol{w}_{ij}$

先为每个样本$\boldsymbol{x}_i$找到其近邻下标集合$Q_i$，然后计算出基于$Q_i$中的样本点对$\boldsymbol{x}_i$进行线性重构的系数$\boldsymbol{w}_i$：

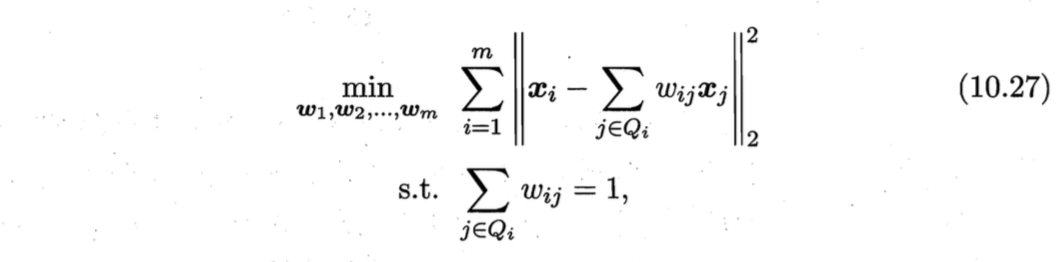
其中，$\boldsymbol{x}_i$和$\boldsymbol{x}j$均为已知，令$C{jk}=(\boldsymbol{x}_i - \boldsymbol{x}_j)^T (\boldsymbol{x}_i - \boldsymbol{x}k)$，$w{ij}$有闭式解

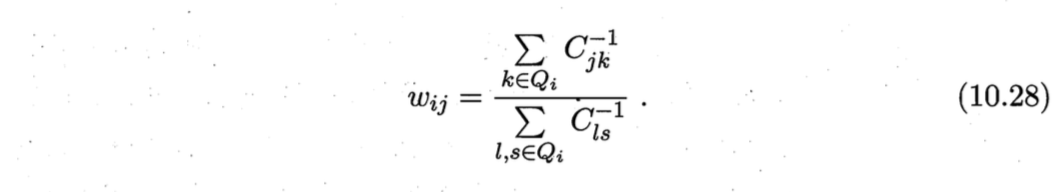
确定对应的低维空间坐标$\boldsymbol{z}_i$

因为LLE在低维空间中保持$\boldsymbol{w}_i$不变，于是$\boldsymbol{x}_i$对应的低维空间坐标$\boldsymbol{z}_i$可通过下式求解：

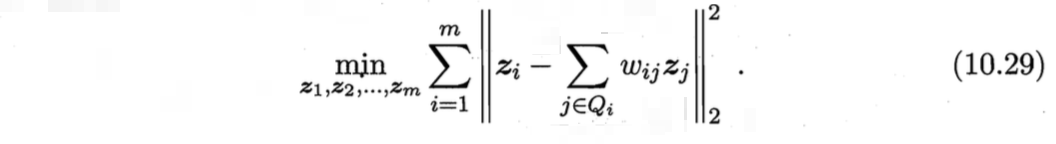
式(10.29)与(10.27)优化目标同形，唯一区别是需确定的变量不同($\boldsymbol{w}_i$和$\boldsymbol{z}_i$)。

令$\boldsymbol{Z} = (z_1,z_2,\cdots, zm) \in \mathbb{R}^{d’ \times m}$, $(\boldsymbol{W}){ij}$ = $w_{ij}$

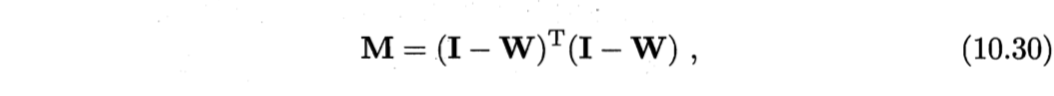
则式(10.29)可重写为

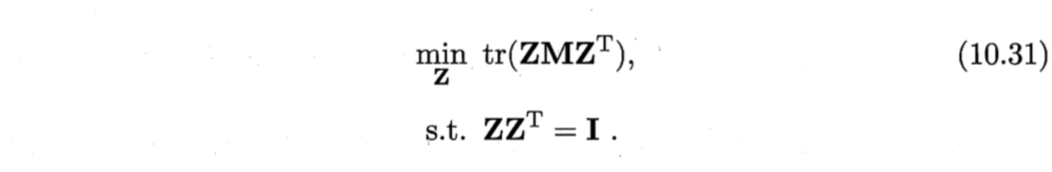
式(10.31)可通过特征值分解求解：$\boldsymbol{M}$最小的$d’$个特征值对应的特征向量组成的矩阵即为$\boldsymbol{Z}^T$。

算法描述

• 4：对于不在样本邻域区域的样本，无论其如何变化都对没有任何影响。

这种将变动限制在局部的思想在许多地方都有用。

10.6 度量学习/距离度量学习(distance metric learning)

基本动机：学习出一个合适的距离度量。

降维的目的是找到合适的低维空间，在该空间中进行学习可以获得更佳性能。实际上，每个空间对应了在样本属性上定义的一个距离度量，寻找合适的低维空间，本本质就是在寻找合适的距离度量。

距离度量的推广

原因：一般的距离度量都没有可供调整的参数，无法通过对样本的学习来改善距离度量。

符号：

• $dist_{ij,k}$：$\boldsymbol{x}_i$和$\boldsymbol{x}_j$在第$k$维上的距离；
• $\boldsymbol{w}$：属性权重，$w_i≥0$；

推广过程：

对两个$d$维样本$\boldsymbol{x}_i$和$\boldsymbol{x}_j$，它们之间的平方欧式距离（欧式距离的平方，为后面推导便利）可写为

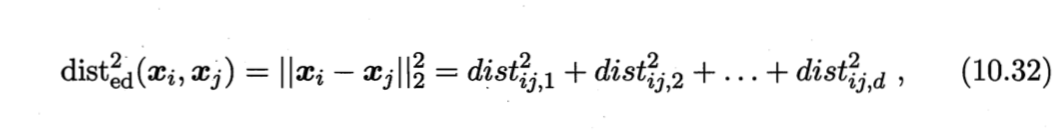
其中，$dist_{ij,k}$表示$\boldsymbol{x}_i$和$\boldsymbol{x}_j$在第$k$维上的距离。若假定不同属性的重要性不同，则可引入属性权重$\boldsymbol{w}$，得到

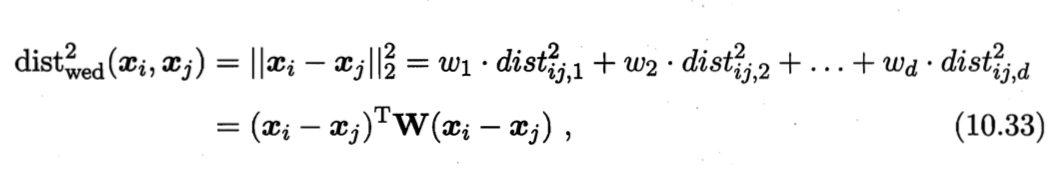
其中，$wi≥0$, $\boldsymbol{W} = diag(\boldsymbol{w})$是一个对角矩阵，$(\boldsymbol{W}){ii} = w_i$。

式(10.33)中的$\boldsymbol{W}$可通过学习确定。

马氏距离(Mahalanobis distance)

假定属性之间相关，即属性对应的坐标轴不正交（$\boldsymbol{W}$的非对角元素均为零，意味着坐标轴正交，即属性之间无关），将$\boldsymbol{W}$替换为一个普通半正定对称矩阵$\boldsymbol{M}$（度量矩阵），即得马氏距离

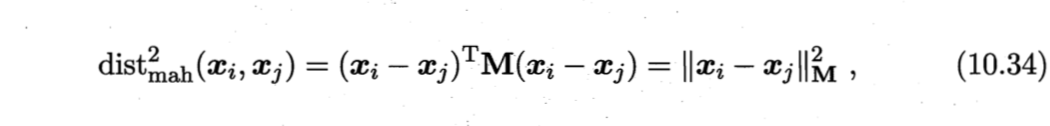
度量学习就是对度量矩阵$\boldsymbol{M}$的学习。为了保证距离的非负性、对称性，$\boldsymbol{M}$必须是(半)正定对称矩阵，即必有正交基$\boldsymbol{P}$使得$\boldsymbol{M} = \boldsymbol{P} \boldsymbol{P}^T$.

马氏距离以印度数学家P.C.Mahalanobis命名。标准马氏距离中$\boldsymbol{M}$是协方差矩阵的逆，即$M=\Sigma^{-1}$；在度量学习中，$M$被赋予更大的灵活性。

求$\boldsymbol{M}$

目标：假定希望提高近邻分类器(Neighbourhood Component Analysis, NCA)[Goldberger et al., 2005]的性能，使LOO正确率最大化。（不同的目标可得不同的$\boldsymbol{M}$）

推导：

求LOO正确率

NCA在进行判别式一般使用多数投票法，邻域中的每个样本投1票，邻域外的样本投0票。为了求$\boldsymbol{M}$，将其替换为概率投票法。对于任意样本$\boldsymbol{x}_j$，它对$\boldsymbol{x}_i$分类结果影响的概率为

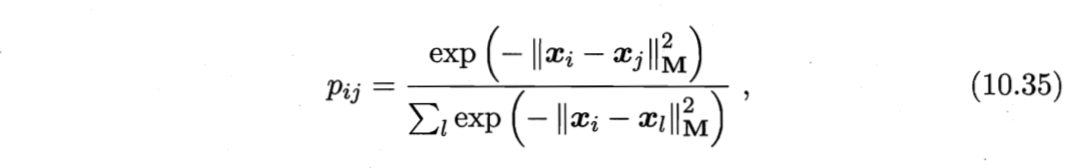
分析：

• 当$i=j$时，$p_{ij}$最大；
• $\boldsymbol{x}_j$对$\boldsymbol{x}_i$的影响随着它们之间距离的增大而减小。

以LOO正确率最大化为目标，则可计算$\boldsymbol{x}_i$的LOO正确率，即它被自身之外的所有样本正确分类的概率为

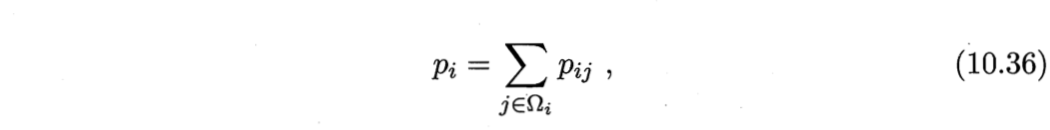
其中，$Ω_i$表示与$\boldsymbol{x}_i$属于相同类别的样本的下标集合。于是，整个样本集上的LOO正确率为

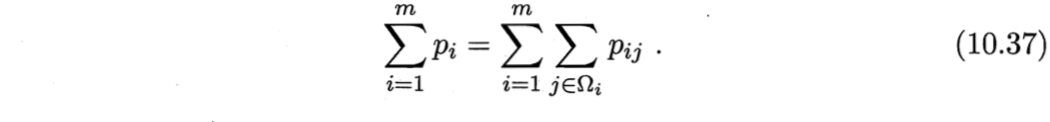
确定NCA的优化目标

将式(10.35)代入(10.37)，再考虑到$\boldsymbol{M} = \boldsymbol{P} \boldsymbol{P}^T$，则NCA的优化目标为

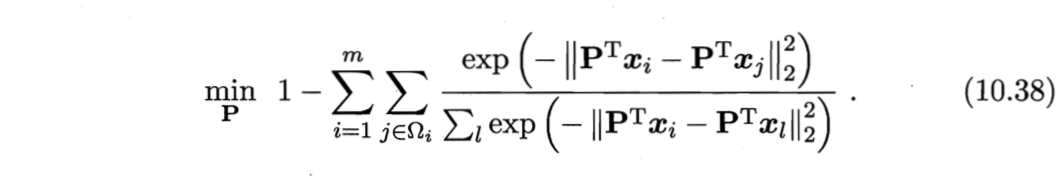
求解(10.38)即可得到最大化NCA的LOO正确率的距离度量矩阵$\boldsymbol{M}$。（可用随机梯度下降法求解）

其他优化目标——领域知识

除了引入LOO，还能在度量学习中引入领域知识。如，若已知某些样本相似、某些样本不相似，则可定义“必连”(must-link)约束集合M与“勿连”(cannot-link)约束集合$C$，$(\boldsymbol{x}_i,\boldsymbol{x}_j)∈M$表示$\boldsymbol{x}_i$与$\boldsymbol{x}_j$相似，$(\boldsymbol{x}_i,\boldsymbol{x}_j)∈ C$表示$\boldsymbol{x}_i$与$\boldsymbol{x}_j$不相似。

自然地，希望相似样本之间距离小、不相似样本间距离大，可得如下凸优化问题来求解度量矩阵M[Xing et al., 2003]：

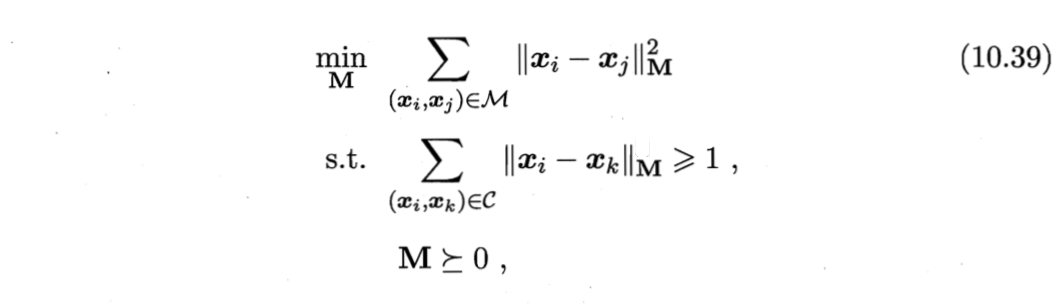
其中，约束$\boldsymbol{M} \succeq 0$表明$\boldsymbol{M}$必须是半正定的. 式(10.39)要求在不相似样本间的距离不小于1的前提下，使相似样本间的距离尽可能小。

降维

若获得的$\boldsymbol{M}$是一个低秩矩阵，则通过对$\boldsymbol{M}$进行特征值分解，总能找到一组正交基，其正交基数目为矩阵$\boldsymbol{M}$的秩$rank(\boldsymbol{M})<d$。于是，度量学习的习得结果可衍生出一个降维矩阵$\boldsymbol{P} \in \mathbb{R}^{d \times rank(M)}$，用于降维目的。