chap 04 - 决策树 | Decision Tree
Contents
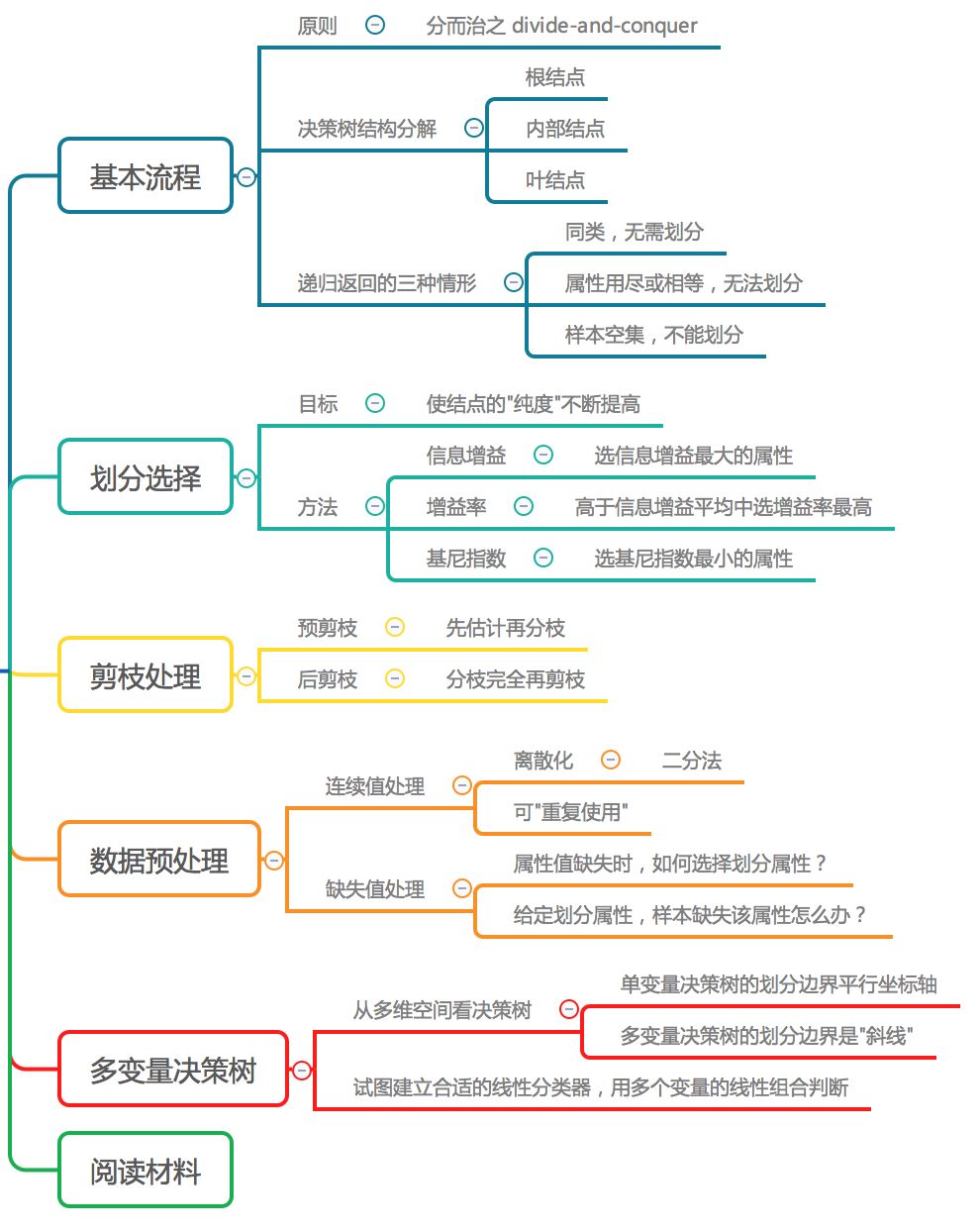
4.1 基本流程
适用任务:分类,以二分类为例
什么是决策树:
- 基于树形结构来进行决策的一种处理过程;
- 经过该处理过程后形成的“决策树”,即决策流程。
决策树分解:
- 先判断什么(父决策),后判断什么(子决策),最后导向什么(最终决策,对应判断结果);
- 属性划分:每个“决策问题”都是对样本“属性”的划分;
- 范围缩小:每个“决策结果”导出的下一步决策都在上一决策的范围内;
- 举一个🌰,挑西瓜的决策树
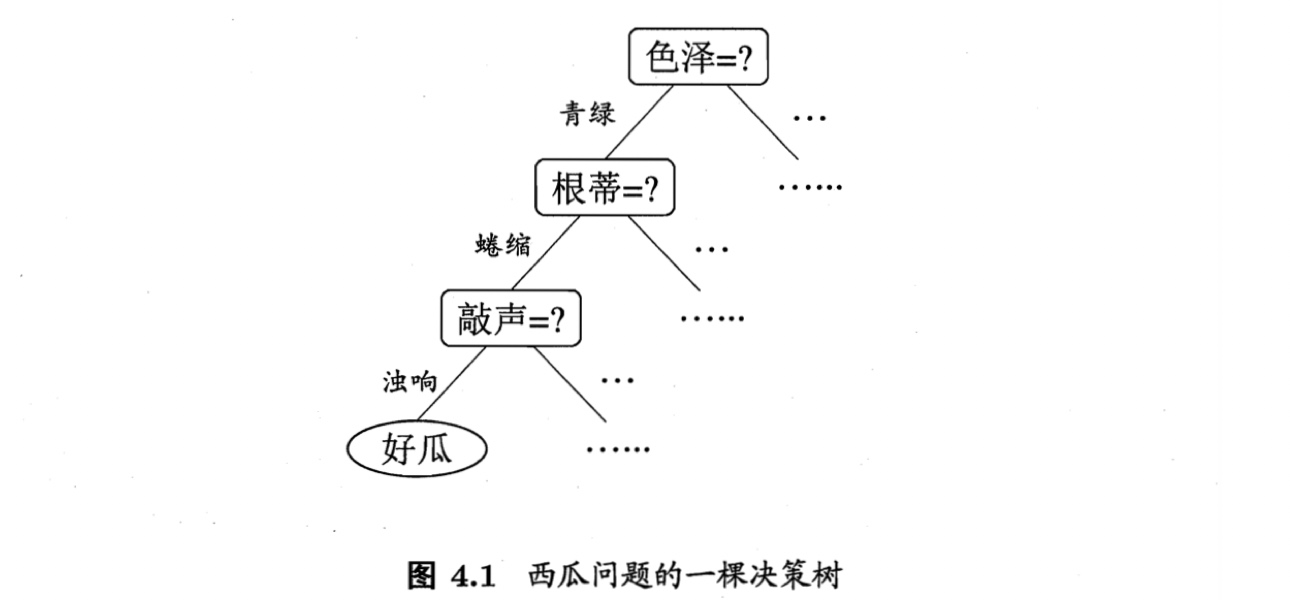
如图,一棵决策树包含
- 一个根结点——第一个决策问题,包含全部样本
- 若干内部结点——决策问题,包含经根节点划分后的部分样本
- 若干叶结点——决策结果,包含的部分样本均属于同一类别
从根节点到每个叶节点的路径对应了一个判定测试序列。
原则: 分而治之 divide-and-conquer
基本流程:

说明: 14. 从A中去掉a*
递归返回情形:
- (1)【Step 03】当前结点包含的样本均属于同一类,无需划分;
- (2)【Step 06】当前属性集为空(属性都用完了),或者所有样本在属性集中取值相同,无法划分;
- (3)【Step 12】当前结点包含的样本集合为空,不能划分。
举🌰:挑西瓜,样本{色泽;根蒂;敲声;甜度;纹理;触感;……)
- (1) 常见
- (2) 属性用完:当前结点的样本均为{色泽=青绿;根蒂=蜷缩;敲声=浊响},类别为(好,坏,好,好,好,坏),N(好)>N(坏),则划分为“好瓜”。
- 取值相同:当前结点的样本{色泽=青绿;根蒂=(蜷缩, 蜷缩,蜷缩,蜷缩 )| (好,坏,好,好)},划分属性A为“根蒂”,样本D在A上的属性值均为“蜷缩”,N(好)>N(坏),所以均划分为“好”。
- (3)上一步结点样本{色泽=青绿;根蒂=(蜷缩, 蜷缩,蜷缩)| (好,坏,好)},原A={色泽,根蒂},且在上一步已使用“色泽”属性划分,此时用“根蒂”划分,根蒂={硬挺, 蜷缩, 稍蜷}
情形2、3的处理:
- (2)把当前结点标记为叶结点,类别设定为该结点所含样本最多的类别.
- (3)把当前结点标记为叶结点,类别设定为其父节点所含类别最多的类别.
情形2、3的区别:
- (2) 利用当前结点的后验分布.
- (3) 把父节点的样本分布作为当前结点的先验分布.
4.2 划分选择
决策树学习的关键:
如何确定最优划分属性?(使分支结点样本的“纯度”purity 高,即,使它们尽量属于同一类别)
4.2.1 信息增益
1️⃣ 信息熵 information entropy
Def:度量样本集合纯度的最常用的一种指标。
假定当前样本集合$D$中第$k$类样本所占比例为$p_k(k=1,2,…,|\cal{Y}|)$,则$D$的信息熵定义为
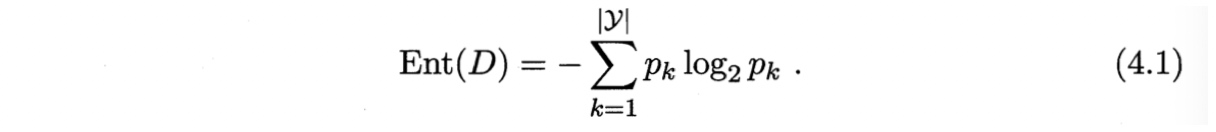 判断方法:$Ent(D)$的值越小,则$D$的纯度越高。
判断方法:$Ent(D)$的值越小,则$D$的纯度越高。
2️⃣ 信息增益 information gain
Def:选择最佳划分属性的依据之一(对应图4.2的Step8),分支前后的信息熵的减小值。
代表方法:ID3决策树算法[Quinlan, 1986]
概念、假设提要:
- 离散属性$a$有$V$个取值,记做${a^1,a^2,…,a^V}$;
- 用属性$a$划分样本集$D$产生$V$个结点,其中第$v$个分支结点包含了$D$中所有在属性$a$上取值为$a^v$的样本,记为$D^v$;
- 给分支节点赋予权重$|D^v|/|D|$(考虑不同的分支结点包含的样本数不同,样本数越多的分支结点的影响越大)
用属性$a$对样本集$D$进行划分所得“信息增益”如下:
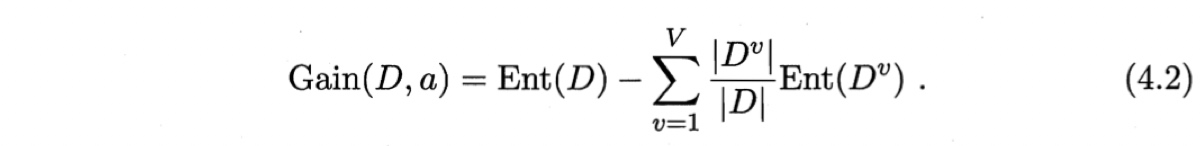
判断方法:Gain(D, a)的值越大,则用属性a划分样本集D带来的纯度提升越大。
具体操作:在图4.2中的Step8采取$a* = {\arg \max}{a \in A} \mathit{Gain}(D,a)$选择划分属性。
举一个例子🌰:
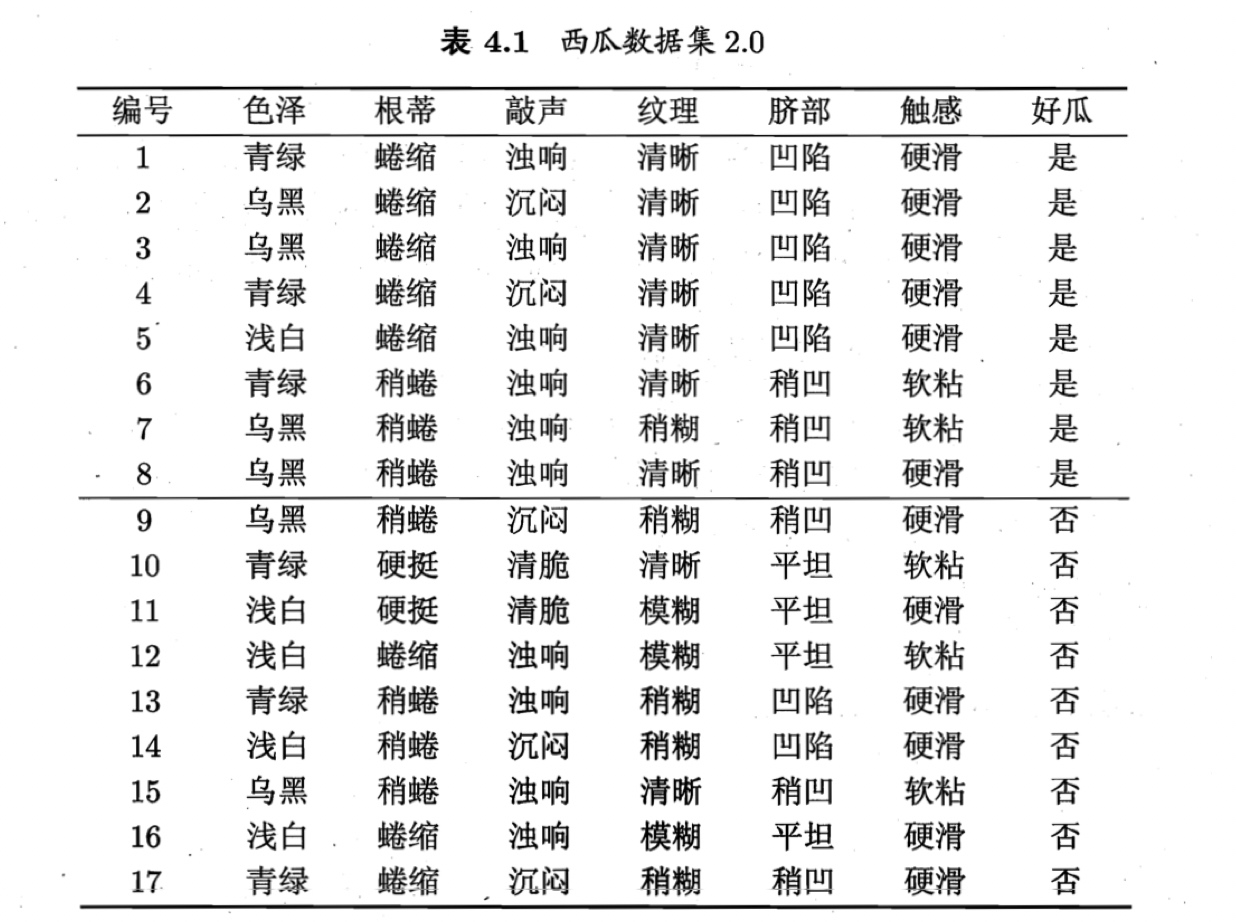
以表4.1中的西瓜数据集2.0为例,该数据集包含17个训练样例,用以学习一棵能预测没剖开的是不是好瓜的决策树.显然$|\mathcal{Y}|=2$.在决策树学习开始时,根结点包含$D$中的所有样例,其中正例占$p_1 = 8.17$,反例占$p_2=\frac{9}{17}$.于是,根据式(4.1)可计算出根结点的信息嫡为
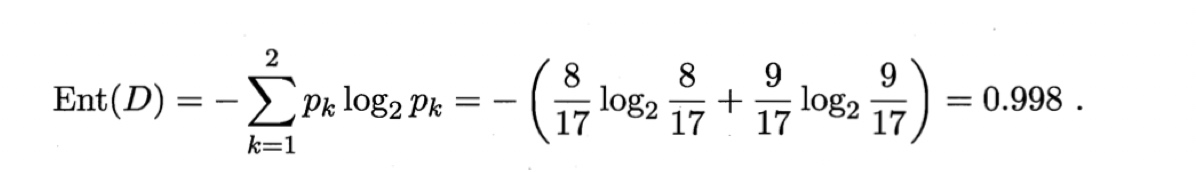 然后,我们要计算出当前属性集合
然后,我们要计算出当前属性集合{色泽,根蒂,敲声,纹理,脐部,触感} 中每个属性的信息增益.以属性“色泽”为例,它有3个可能的取值:{青绿,乌 黑,浅白}.若使用该属性对$D$进行划分,则可得到3个子集,分别记为:$D^1$(色 泽=青绿),$D^2$(色泽=乌黑),$D^3$(色泽=浅白). 子集$D^1$包含编号为{{1, 4, 6, 10, 13, 17}的6个样例,其中正例占$p_1=\frac{3}{6}$, 反例占$p_2=\frac{3}{6}$;$D^2$包含编号为{2,3,7,8,9,15}的6个样例,其中正、反例分别占$p_1=\frac{4}{6}, p_2=\frac{2}{6}$;$D^3$包含编号为{5, 11, 12, 14, 16}的5个样例,其中正、反例分别占$p_1=\frac{1}{5}, p_2=\frac{4}{5}$.根据式(4.1)可计算出用“色泽”划分之后所获得 的3个分支结点的信息嫡为
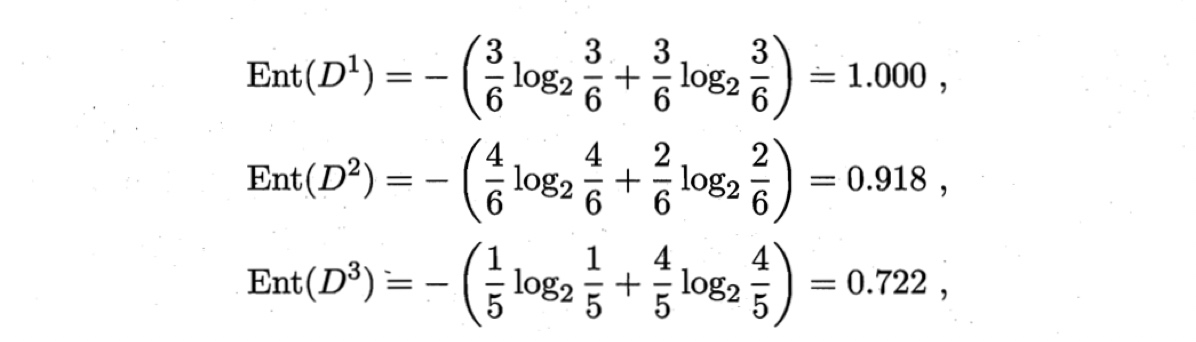
于是,根据式(4.2)可计算出属性“色泽”的信息增益为
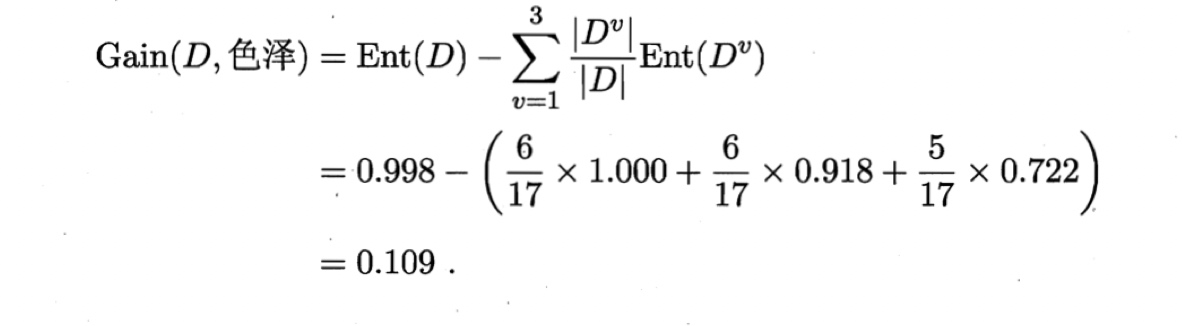 类似的,我们可计算出其他属性的信息增益:
类似的,我们可计算出其他属性的信息增益:

显然,属性“纹理”的信息增益最大,于是它被选为划分属性.图4.3给出了基于“纹理”对根结点进行划分的结果,各分支结点所包含的样例子集显示在结点中.
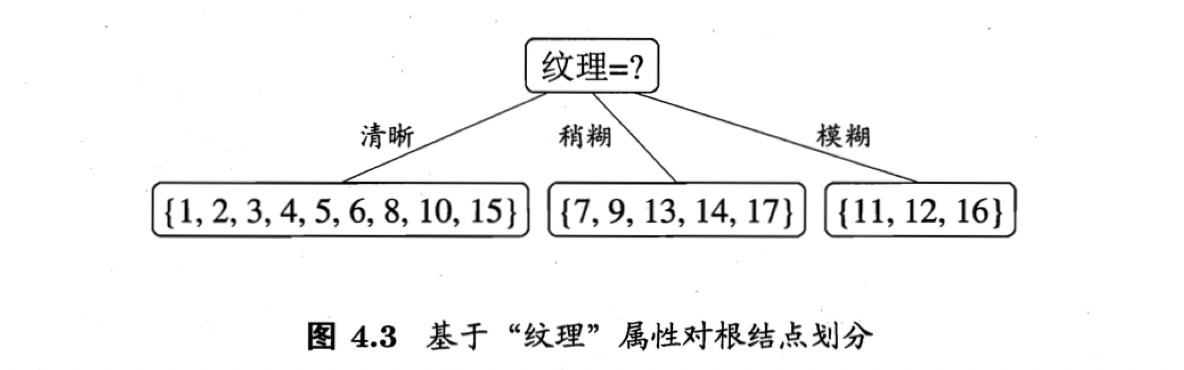
然后,决策树学习算法将对每个分支结点做进一步划分.以图4.3中第一个分支结点(“纹理=清晰”)为例,该结点包含的样例集合$D^1$中有编号为{1, 2, 3, 4, 5, 6, 8, 10, 15}的9个样例,可用属性集合为{色泽,根蒂,敲声,脐部, 触感}.基于$D^1$计算出各属性的信息增益:

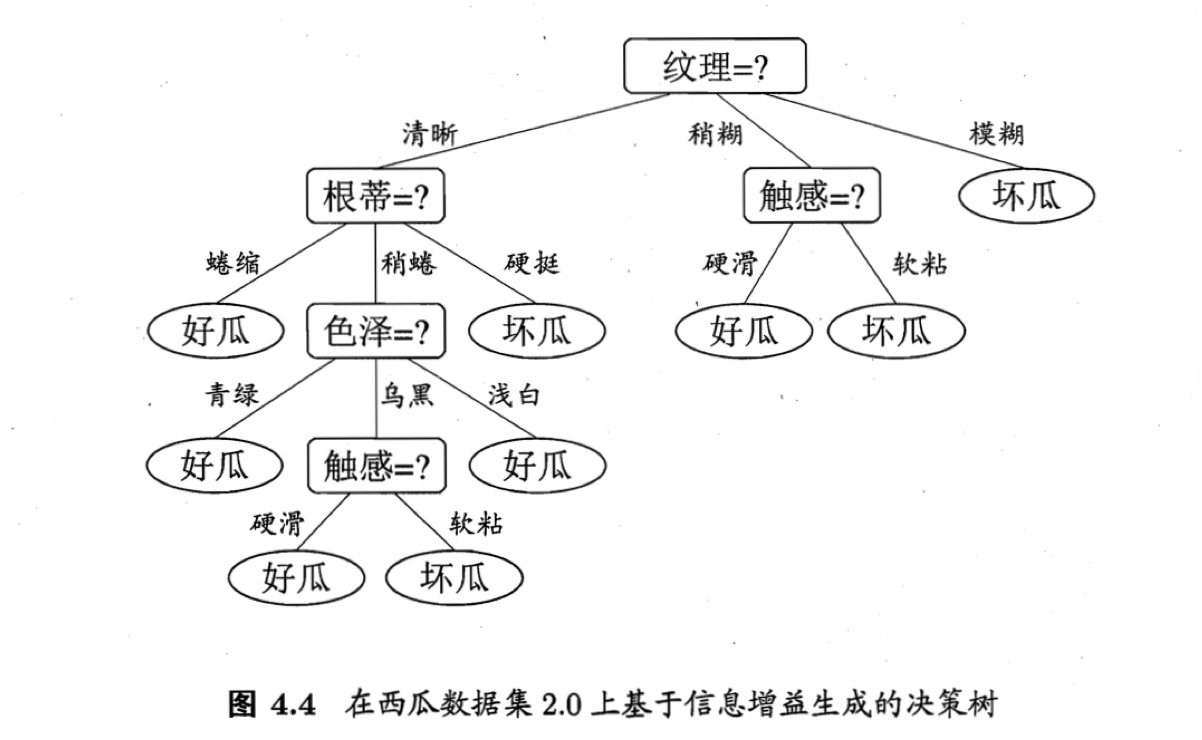
“根蒂”、“脐部”、“触感”3个属性均取得了最大的信息增益,可任选其中之一作为划分属性.类似的,对每个分支结点进行上述操作,最终得到的决策树如图4.4所示.
4.2.2 增益率 gain ratio
Def:
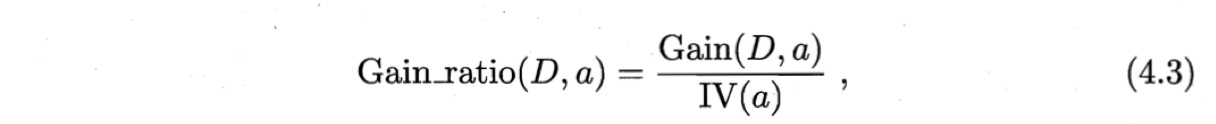
符号说明:
- $IV(a)$ :属性a的固有值 intrinsic value,$a$的可能取值数目越多($V$越大),$IV(a)$越大;
- $Gain(D, a)$:用属性$a$对样本集$D$进行划分所得“信息增益”。
以前方法缺陷:
信息增益偏好“可取值数目较多”的属性,(如,若将编号也纳入可选属性,则决策树会产生17个分支,每个分支都在训练集上绝对正确。得出的决策树不具备泛化能力!)
代表方法: C4.5决策树算法[Quinlan, 1993]
注意: 增益率准则偏好可取值数目较少的属性,增加了属性取值数目的惩罚项。
具体操作:
C4.5算法并不是直接选取增益率最大的属性,而是使用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。(高于平均中选最高)
例子🌰:
对表4.1的西瓜数据集2.0,有 IV(触感)=0.874(V=2),IV(色泽)=1.580(V=3),IV(编号)=4.088(V=17)
4.2.3 基尼系数 Gini index
代表方法: CART (Classification and Regression Tree)决策树算法 [Breiman et al., 1993]
符号说明:
1. 基尼值:衡量数据集$D$的纯度指标,$Gini(D)$越小,数据集$D$纯度越高。
 1. 属性$a$的基尼指数:
1. 属性$a$的基尼指数:
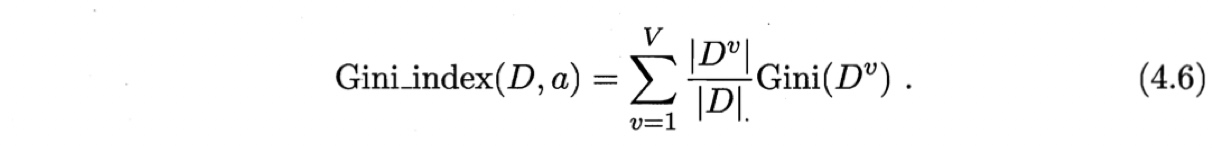
具体操作:
在候选属性集A中,选择使划分后Giniindex最小的属性$a^*$作为最优划分属性,即$a* = {\arg \min}_{a \in A} \mathit{Gini_index} (D,a)$
三种划分标准的区别
在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益比来选择特征,以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。
能不能简化模型同时也不至于完全丢失熵模型的优点呢?有!CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。
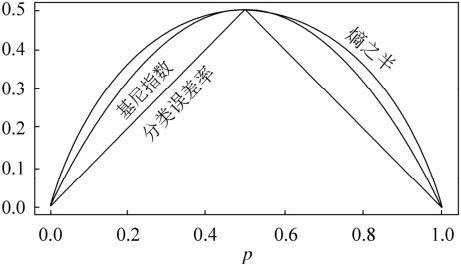
从上图可以看出,基尼系数和熵之半的曲线非常接近,仅仅在45度角附近误差稍大。因此,基尼系数可以做为熵模型的一个近似替代。而CART分类树算法就是使用的基尼系数来选择决策树的特征。同时,为了进一步简化,CART分类树算法每次仅仅对某个特征的值进行二分,而不是多分,这样CART分类树算法建立起来的是二叉树,而不是多叉树。这样一可以进一步简化基尼系数的计算,二可以建立一个更加优雅的二叉树模型。
4.3 剪枝 pruning 处理
- def(剪枝):决策树算法对抗
“过拟合”的主要手段。训练中不断产生的分支可能不仅学到了样本集的一般性质,还学到了特殊性质,所以通过主动去掉一些分支来降低过拟合风险。
基本策略:[Quinlan, 1993]
- 预剪枝 pre-pruning:在决策树生成过程中,每生成一个新的分支就判断其能否增强决策树的泛化能力,不能则停止划分并标记当前节点为叶结点。
- 后剪枝 post-pruning:先用训练集生成一棵完整的决策树,然后自底向上考察每一个节点,若将该节点对应的子树替换为叶结点(就像是剪断树枝的一个分叉点,就剪掉了一丛树枝)能提升泛化能力,则进行替换。
如何判断“泛化性能提升”——性能评估法(2.2节):
- 本节采取留出法,预留一部分数据作为“验证集”进行评估。
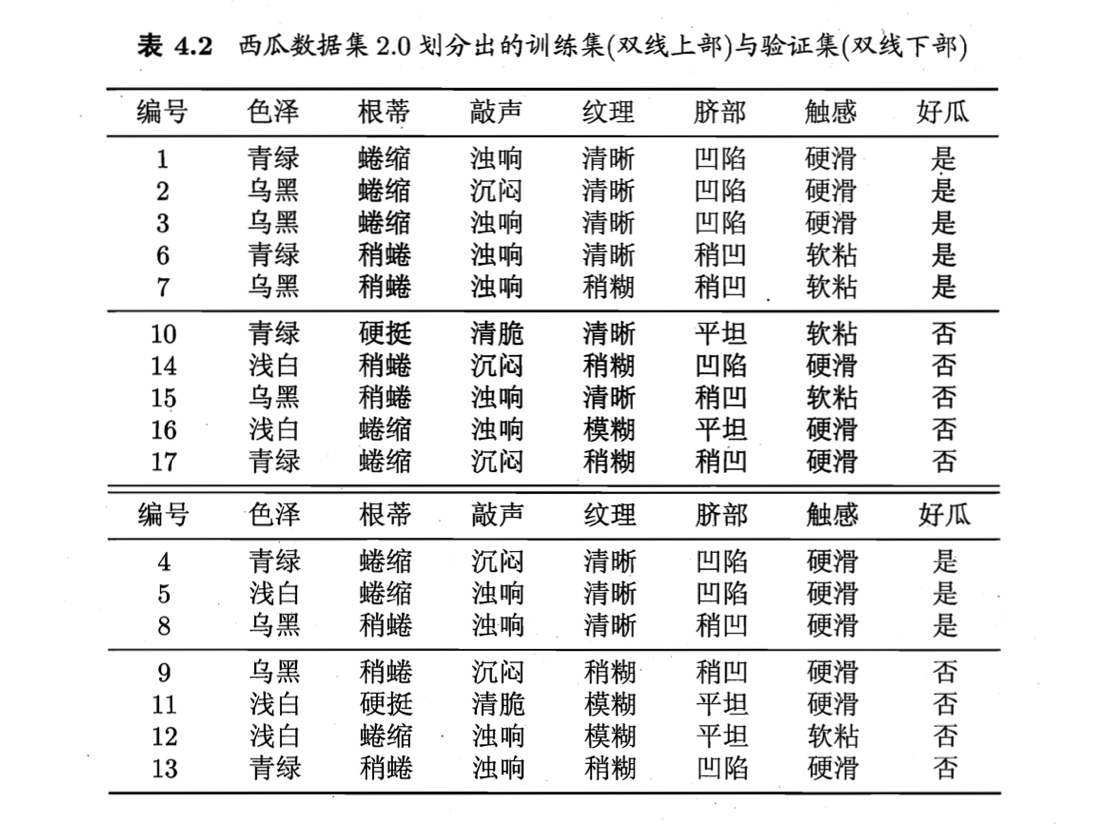
例如对表4.1的西瓜数据集2.0,我们将其随机划分为两部分,如表4.2所示,编号为{1,2,3,6,7, 10, 14, 15, 16, 17}的样例组成训练集,编号为 {4, 5, 8, 9, 11, 12, 13}的样例组成验证集.
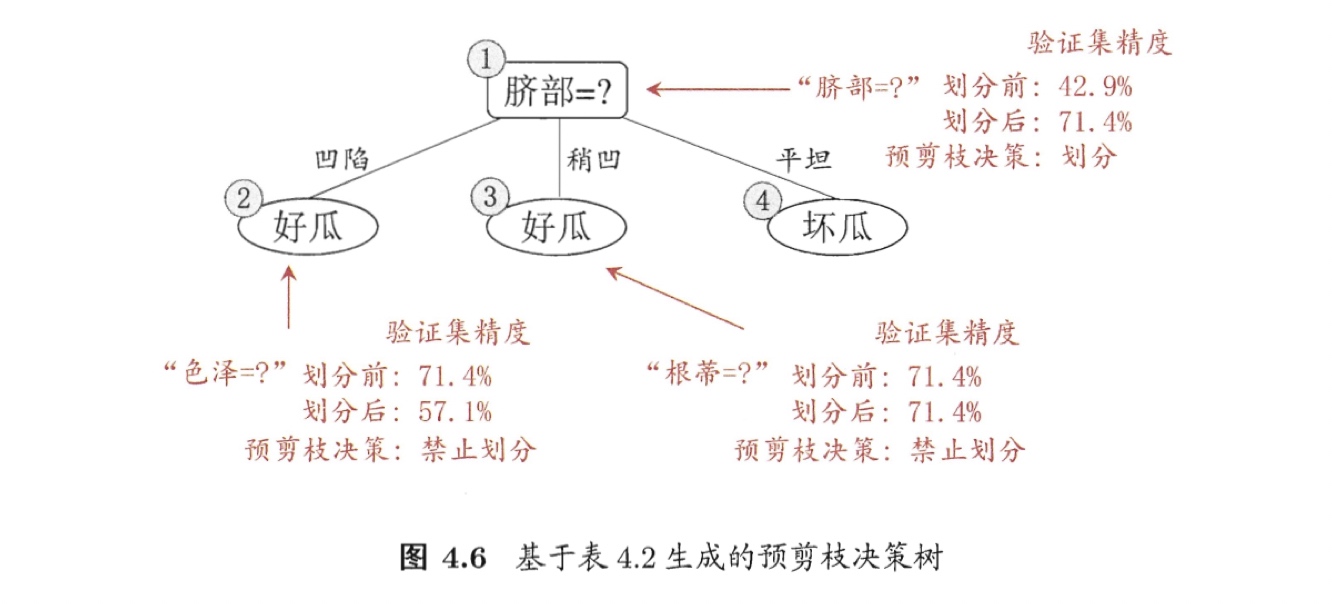
假定我们采用4.2.1节的信息增益准则来进行划分属性选择,则从表4.2的训练集将会生成一棵如图4.5所示的决策树.为便于讨论,我们对图中的部分结点做了编号.
以下均以此例说明:
4.3.1 预剪枝 pre-pruning
优点:
- 决策树很多分支都没有展开,降低过拟合风险,显著减少训练时间开销;
缺点:
- 未展开的分支虽不能提升决策树泛化性能,但在其基础上进行的后续划分可能导致性能显著提高,预剪枝使我们失去了这样的机会;
- 基于“贪心”本质禁止分支展开,带来了“欠拟合”风险。
步骤演示:
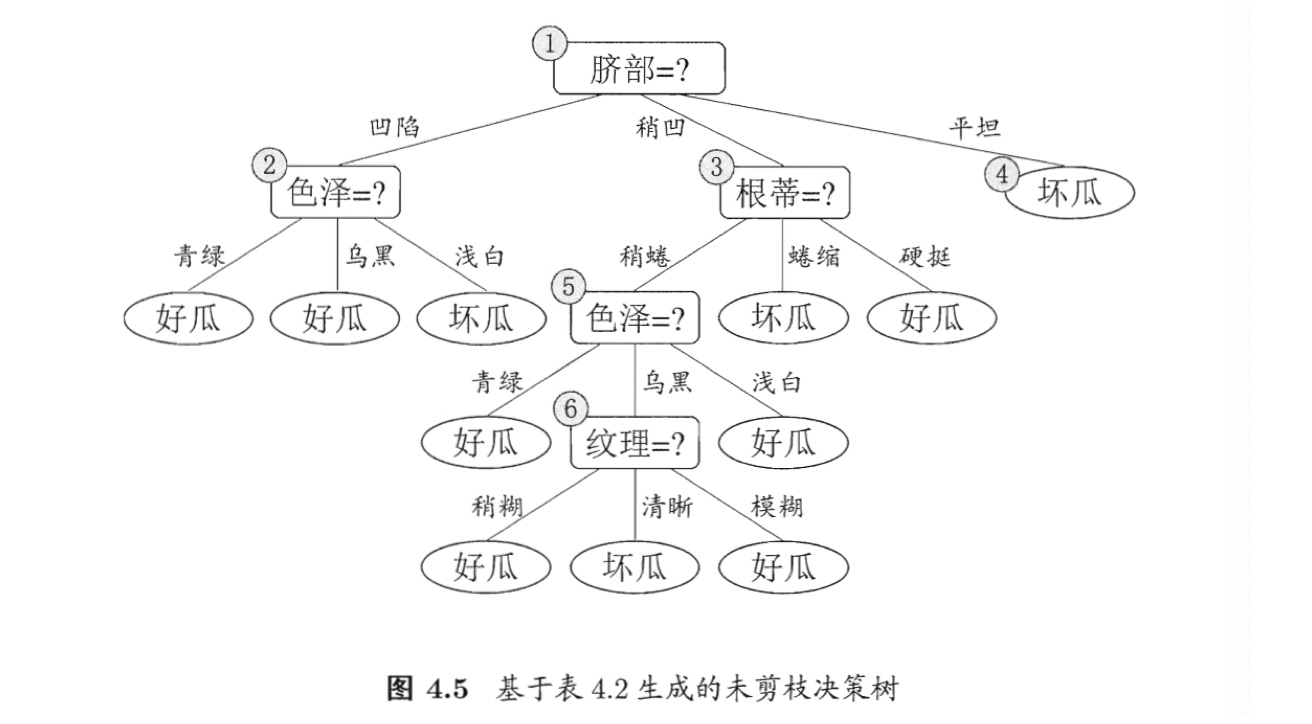
- 基于信息增益准则,应选取属性“脐部”对训练集划分,产生3个分支,如图4.6。
- 预剪枝判断是否应进行分割①:
- (1)若不划分,根据图4.2决策树学习基本算法,标记根节点为叶结点,类别为样例最多类别,因为N(正)=N(反),假设将此结点标记为“好瓜”。用表4.2的验证集评估,{4,5,8}分类正确,验证集精度为3/7 × 100% = 42.9%。
- (2)若划分,图4.6中结点②、③、④分别包含编号为{1,2,3,14}、{6,7,15,17}、{10,16}的训练样本,三个结点依次被标记为“好瓜”、“好瓜”、“坏瓜”。{4,5,8,11,12}分类正确,验证集精度为5/7 × 100% = 71.4% 。
- (3)判断,验证集精度71.4%> 42.9%,确定用“脐部”属性划分。
- 依次对结点②、③、④进行预剪枝判断:
- (1)②:基于信息增益准则,选取属性“色泽”;但划分后,样本{5}分类结果由正确转为错误,验证集精度下降至57.1%;禁止划分。
- (2)③:基于信息增益准则,选取属性“根蒂”;但划分后,验证集精度仍为71.4%,没有提高;禁止划分。
- (3)④:所含训练样例已属于同一类;不再划分。
- 得出决策树如图4.6所示,验证集精度为71.4%。这是一颗只有一层划分的决策树,亦称“决策树桩”(decision stump)。
4.3.2 后剪枝 post-pruning
优点:
- 一般情况下,后剪枝决策树欠拟合风险小,泛化性能由于预剪枝决策树。
缺点:
- 相比预剪枝保留了更多分支,且要先生成完全决策树,再自底向上一一考察结点,因此训练时间开销>>未剪枝决策树、预剪枝决策树。
步骤演示:
从训练集生成一棵完整的决策树,如图4.5,其验证集精度为42.9%;
从底向上考察结点,先考察⑥:
- (1)若将其领衔的分支剪除,即把⑥结点替换为叶结点,则替换后的结点包含{7,15}训练样本,该叶结点被标记为“好瓜”;
- (2)判断精度,此时精度提高到57.1%,所以确定剪除⑥。
再考察⑤:
- (1)若把⑤结点替换为叶结点,则替换后的叶结点包含{6,7,15}训练样本,被标记为“好瓜”;
- (2)判断精度,此时精度仍为57.1%,可以不剪除⑤。
- 注:根据奥卡姆剃刀原则,应予剪枝。为了绘图方便,采取了不剪枝的保守策略。
考察结点②:
- (1)若把②结点替换为叶结点,则替换后的叶结点包含{1,2,3,14}训练样本,被标记为“好瓜”;
- (2)判断精度,此时精度提高至71.4%,剪除②。
考察结点③和①:
- (1)若把③或①结点替换为叶结点,则……;
- (2)判断精度,此时精度分别为71.4%与42.9%,均未提高,保留③和①。
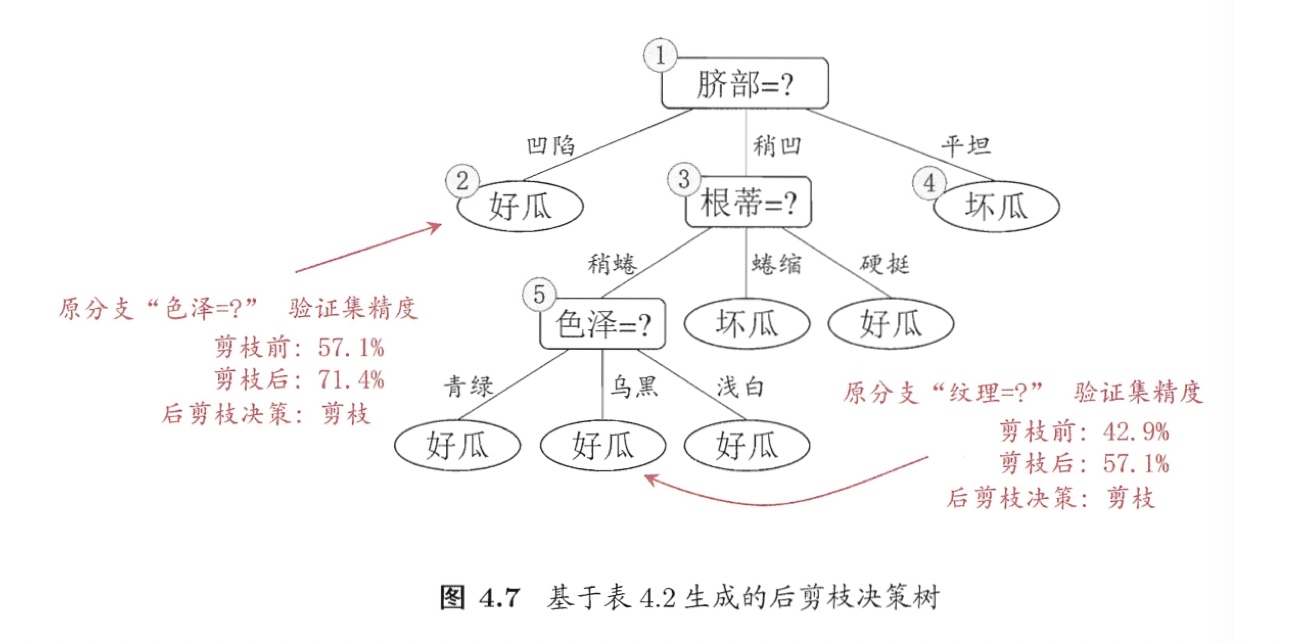
注:④已经是叶结点,不用后剪枝判断。
4.4 连续与缺失值
4.4.1 连续值处理
连续属性的特点:
- 可取值数目无限,不能逐一划分。
- 要进行离散化处理。
最简单策略:二分法 bi-partition
算法代表:C4.5决策树算法 [Quinlan, 1993]
与离散属性的区别:若当前节点划分属性为连续属性,该属性还可以作为其后代节点的划分属性。即,可“重复”使用。
操作过程:
给定样本集$D$、连续属性$a,假设$a$在$D$上有$n$个不同取值。
- 将$a$的$n$个取值从小到大排序,记为${a^1,a^2, … ,a^n}$;
考察包含$n-1$个元素的候选划分点集合,把区间$[a^i,a^{i+1})$的中位点$\frac{a^i + a^{i+1}}{2}$作为候选划分点
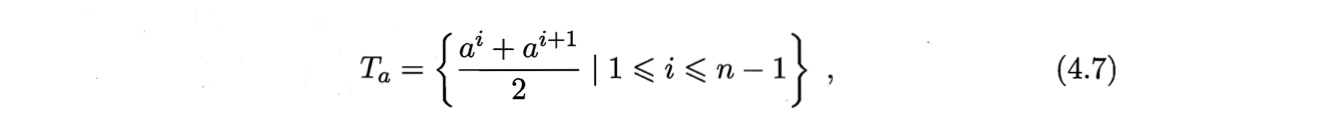
类似离散属性值,考察划分点,选取最优划分点对样本集合进行划分。如,考察
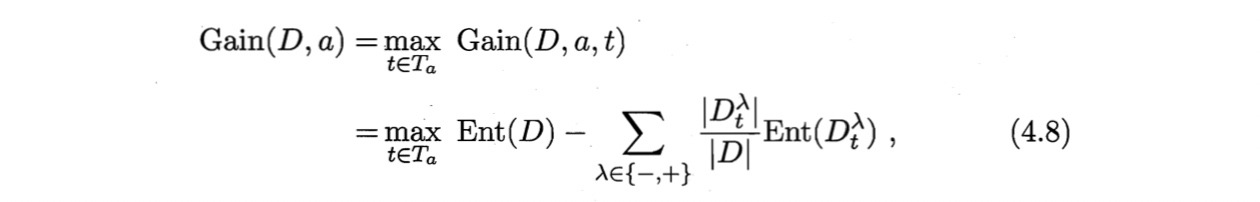 其中$Gain(D, a, t)$是样本集$D$基于划分点$t$二分后的信息增益。选择使$Gain(D, a, t)$最大化的划分点。
其中$Gain(D, a, t)$是样本集$D$基于划分点$t$二分后的信息增益。选择使$Gain(D, a, t)$最大化的划分点。
给定样本集$D$和连续属性$a$,假定$a$在$D$上出现了$n$个不同的取值,将这些值从小到大进行排序,记为${a^1,a^2,\cdots,a^n}$.基于划分点$t$可将$D$分为子集$D_t^+$和$D_t^-$,其中$D_t^+$包含那些在属性$a$上取值不大于$t$的样本,而$D_t^-$才则包含那些在属性$a$上取值大于$t$的样本.显然,对相邻的属性取值$a^i$来说,$t$在区间$[a^i,a^{i+1})$中取任意值所产生的划分结果相同.
举个例子🌰:
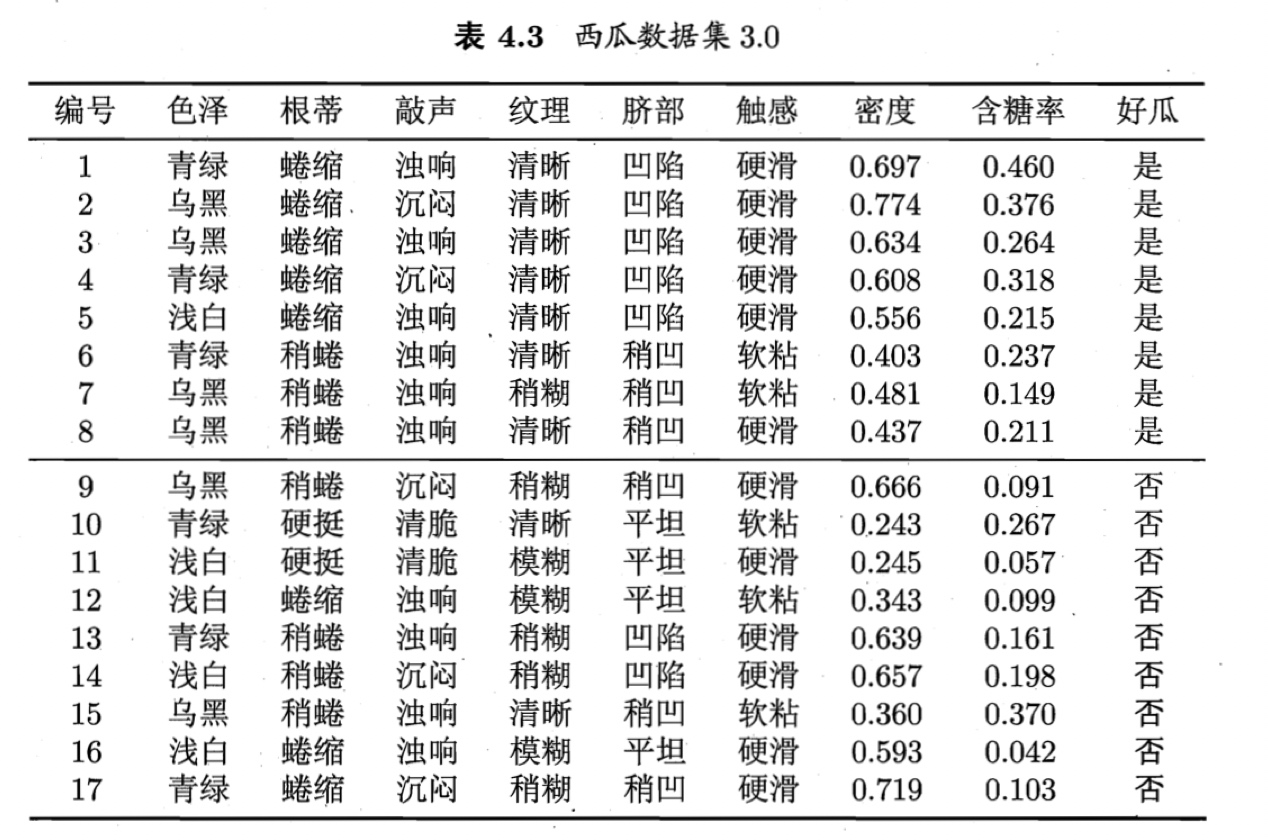
作为一个例子,我们在表4.1的西瓜数据集2.0上增加两个连续属性“密度”和“含糖率”,得到表4.3所示的西瓜数据集3.0. 下面我们用这个数据集来生成一棵决策树.
对属性“密度”,在决策树学习开始时,根结点包含的17个训练样本在该属性上取值均不同.根据式(4.7),该属性的候选划分点集合 包含16个候选值:$T_{密度}$={0.244, 0.294, 0.351, 0.381, 0.420, 0.459, 0.518, 0.574, 0.600, 0.621, 0.636, 0.648, 0.661, 0.681, 0.708, 0.746}.由式(4.8)可计算出属性“密度”的信息增益为0.262,对应于划分点0.381.
对属性“含糖率”,其候选划分点集合也包含16个候选值:$T_{含糖率}$= {0 .049, 0.074,0.095,0.101,0.126, 0.155,0.179, 0.204, 0.213,0.226, 0.250, 0.265, 0.292, 0.344, 0.373, 0.418}.类似的,根据式(4.8)可计算出其信息增益为0.349, 对应于划分点0.126.
再由4.2.1节可知,表4.3的数据上各属性的信息增益为

于是,“纹理”被选作根结点划分属性,此后结点划分过程递归进行,最终 生成如图4.8所示的决策树.
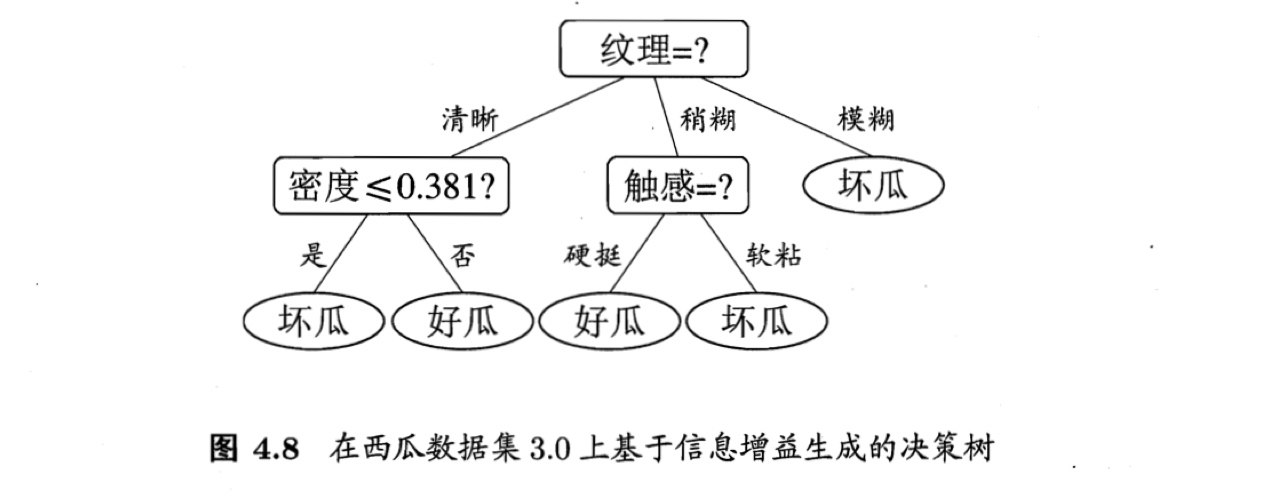
4.4.2 缺失值处理
背景问题:
- 现实中样本缺失属性很常见(如由于诊测成本、隐私保护等因素,患者的医疗数据在某些属性上的取值(如HIV测试结果)未知);
- 样本属性较多时,往往会有大量样本出现缺失值;
- 直接放弃不完整样本只研究完整样本是对数据信息的极大浪费。
举一个例子🌰:
表4.4中,共有17个样本,其中仅有4个样本没有缺失值。
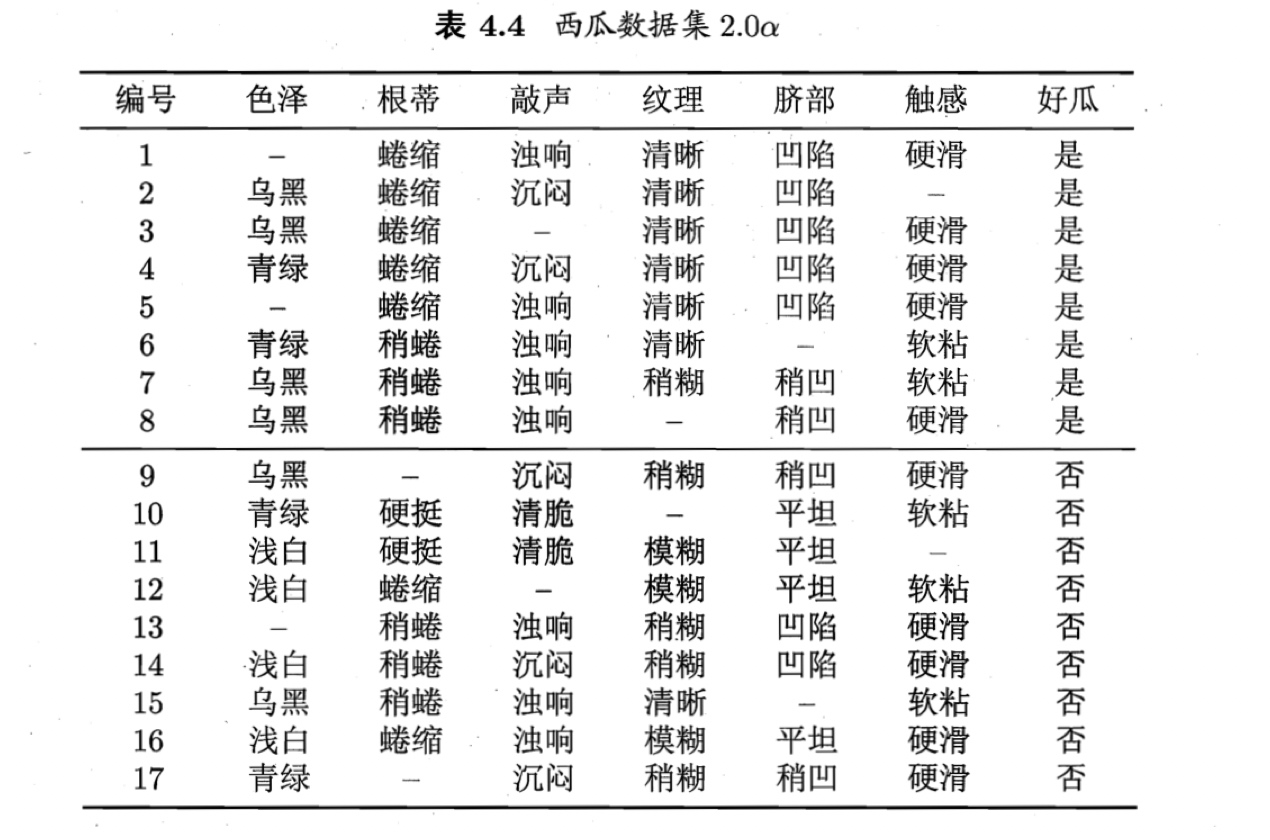
待解决的两个问题:
- (1)如何在属性值缺失的情况下进行划分属性选择?
- (2)给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分?
符号及假设:
- 训练集$D$,属性$a$;
- $\tilde{D}$表示$D$中在属性$a$上没有缺失的样本子集;
- $\tilde{D}^v$表示$\tilde{D}$中在属性$a$上取值为$a^v$的样本子集;
- $\tilde{D}k$表示$\tilde{D}$中属于第$k$类$(k=1,2,\cdots, |\mathcal{Y}|)$的样本子集,则显然有$\tilde{D} = \cup{k=1}^{\mathcal{Y}} \tilde{D}k$,$\tilde{D} = \cup{v=1}^V \tilde{D}^v$,
问题1️⃣: 仅可根据$\tilde{D}$来判断属性$a$的优劣。
假定对每个样本$x$赋予权重$w_x$,并定义:
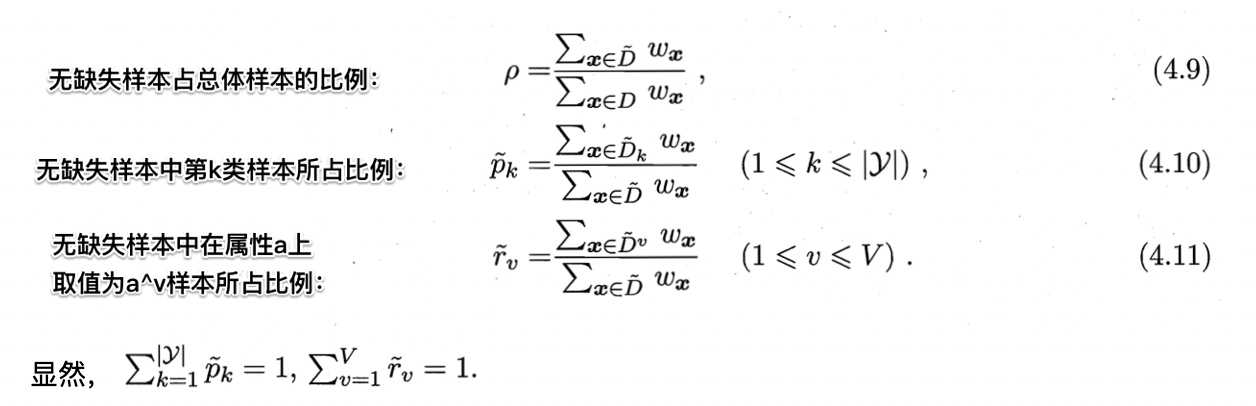
基于上述定义,把信息增益推广为:
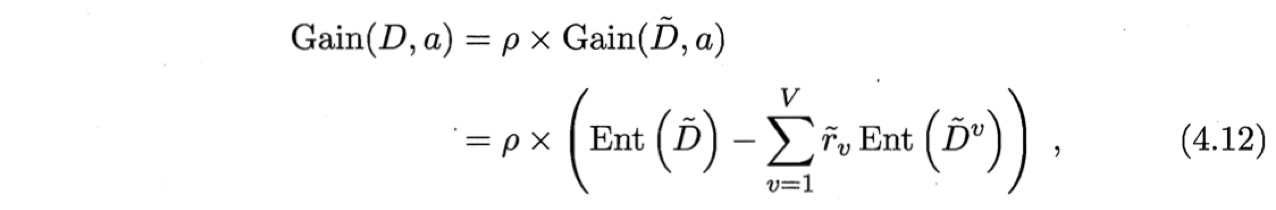 其中,由式(4.1),有
其中,由式(4.1),有
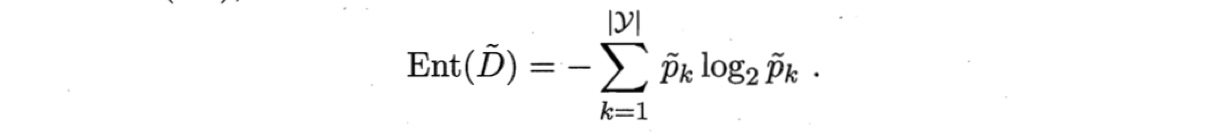
问题2️⃣:
- 若样本$x$在划分属性$a$上的取值已知,则将$x$划入与其取值对应的子节点,且样本权值在子节点中保持为$w_x$;
- 若样本x在划分属性a上的趋势位置,则将x同时划入所有子节点,且样本权值在与属性值$a^v$对应的子节点中调整为 $\tilde{r}_v \cdot w_x$(直观上看,就是让同一个样本以不同概率划到不同的子节点中去)。
举一个例子🌰:
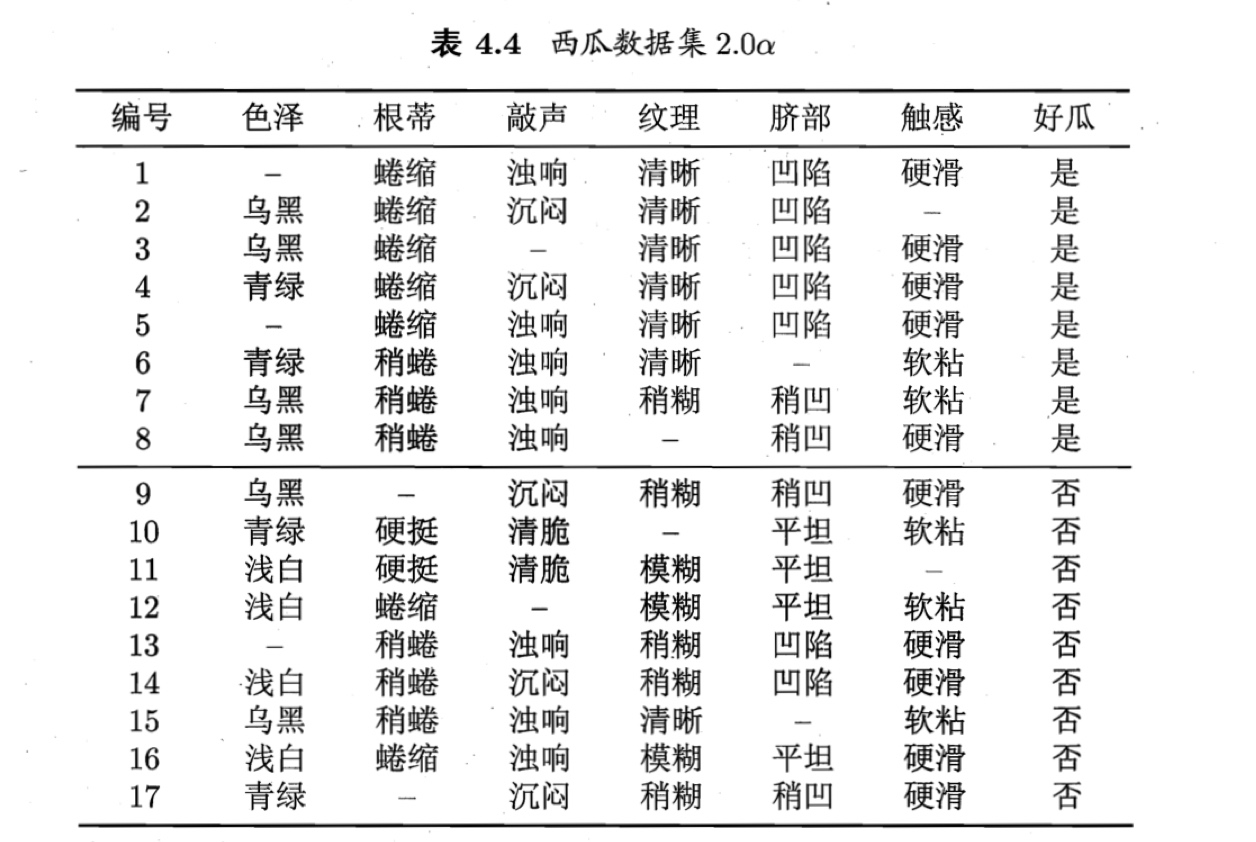
C4.5算法使用了上述解决方案[Quinlan, 1993].下面我们以表4.4的数据集为例来生成一棵决策树.在学习开始时,根结点包含样本集$D$中全部$17$个样例,各样例的权值均为$1$.以属性“色泽”为例,该属性上无缺失值的样例子集$\tilde{D}$包含编号为 {2,3,4,6,7,8,9, 10, 11, 12,14, 15, 16, 17}的14个样例.显然,$\tilde{D}$的信息嫡为
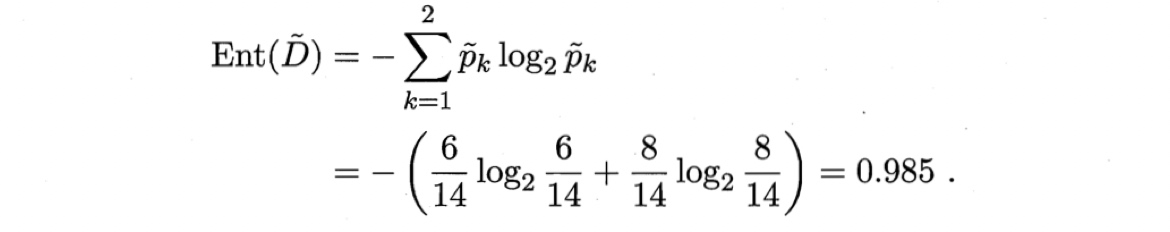 令$\tilde{D}^1$,$\tilde{D}^2$与$\tilde{D}^3$分别表示在属性“色泽”上取值为“青绿”“乌黑”以及“浅白”的样本子集,有
令$\tilde{D}^1$,$\tilde{D}^2$与$\tilde{D}^3$分别表示在属性“色泽”上取值为“青绿”“乌黑”以及“浅白”的样本子集,有
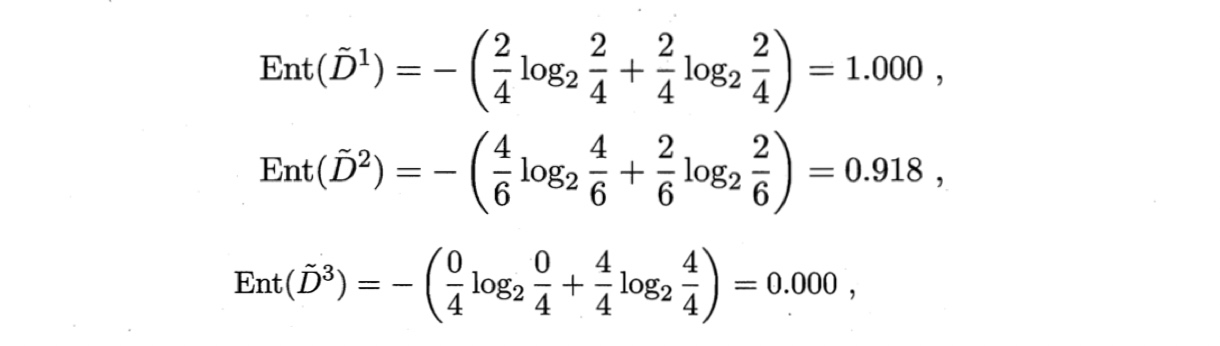 因此,样本子集$\tilde{D}$上属性“色泽”的信息增益为
因此,样本子集$\tilde{D}$上属性“色泽”的信息增益为
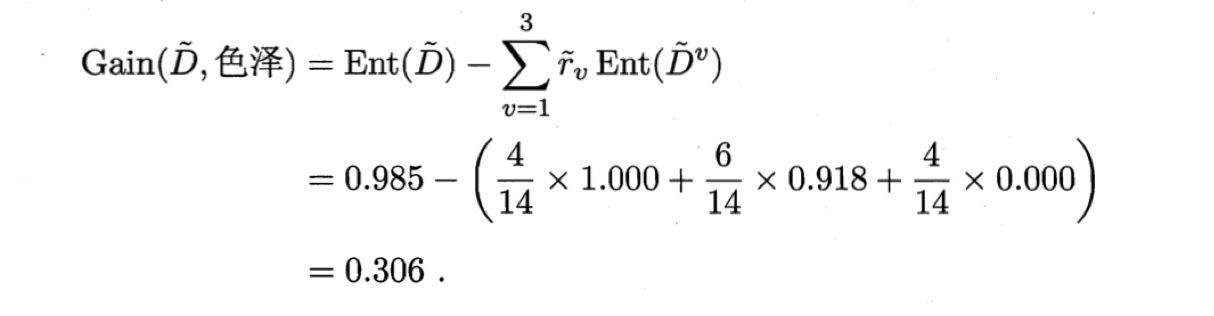
于是,样本集D上属性“色泽”的信息增益为
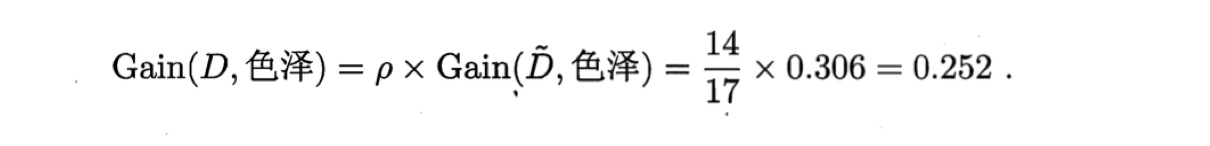
类似地可计算出所有属性在D上的信息增益:

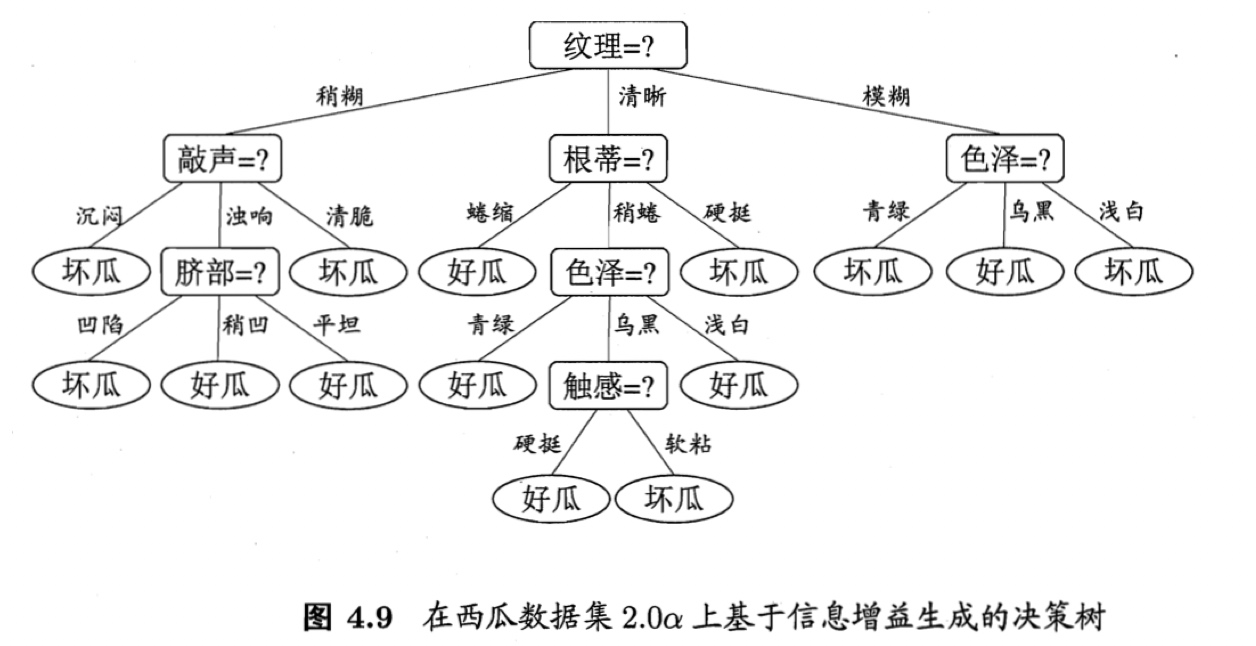
“纹理”在所有属性中取得了最大的信息增益,被用于对根结点进行划分.划分结果是使编号为{1,2,3,4,5,6,15}的样本进入“纹理=清晰”分支,编号为{7, 9, 13, 14, 17}的样本进入“纹理=稍糊”分支,而编号为{11, 12, 16}的样本进入“纹理=模糊”分支,且样本在各子结点中的权重保持为1.需注意的是,编号为{8}的样本在属性“纹理”上出现了缺失值,因此它将同时进入三个分支中,但权重在三个子结点中分别调整为$7⁄15$、$5⁄15$和$3⁄15$.编号为{10}的样本有类似划分结果.
上述结点划分过程递归执行,最终生成的决策树如图4.9所示.
4.5 多变量决策树
从多维空间看决策树划分样本:
- 若我们把每个属性视为坐标空间中的一个坐标轴,则d个属性描述的样本就对应了d维空间中的一个数据点,对样本分类则意味着在这个坐标空间中寻找不同样本之间的分类边界。
- 决策树形成的边界有一个明显特点:轴平行 axis-parallel,即它的分类边界由若干个与坐标轴平行的分段组成。
举一个例子🌰:
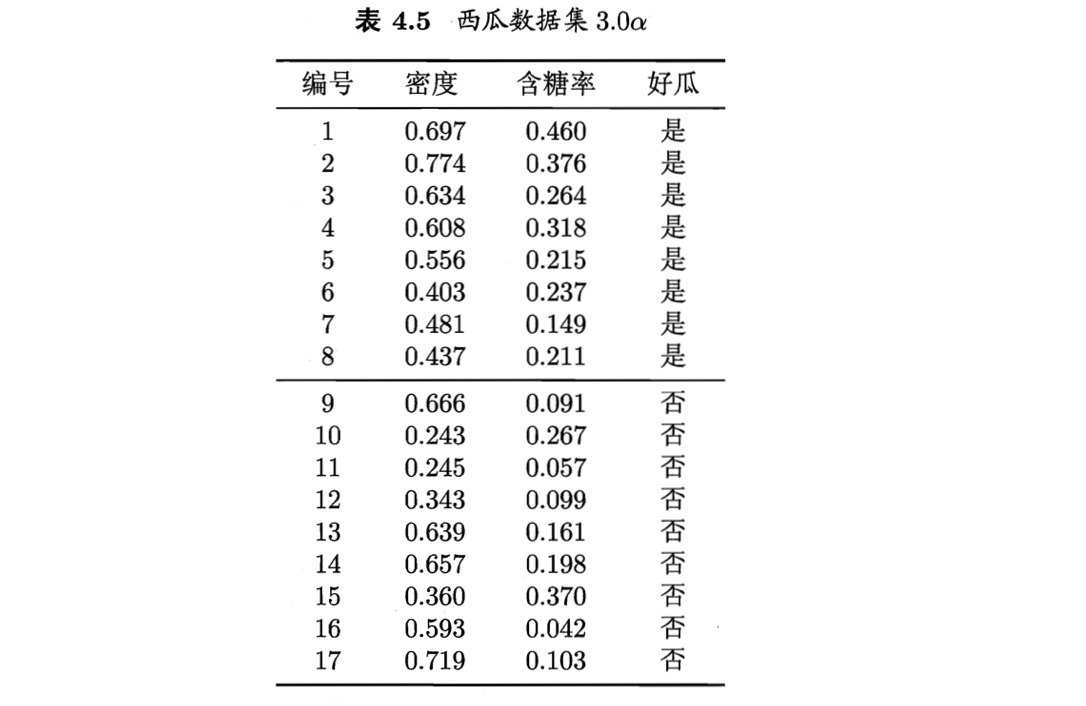
以表4.5中的西瓜数据3.0α为例,将它作为训练集可习得图4.10所示决策树,决策树对应的分类边界如图4.11所示。
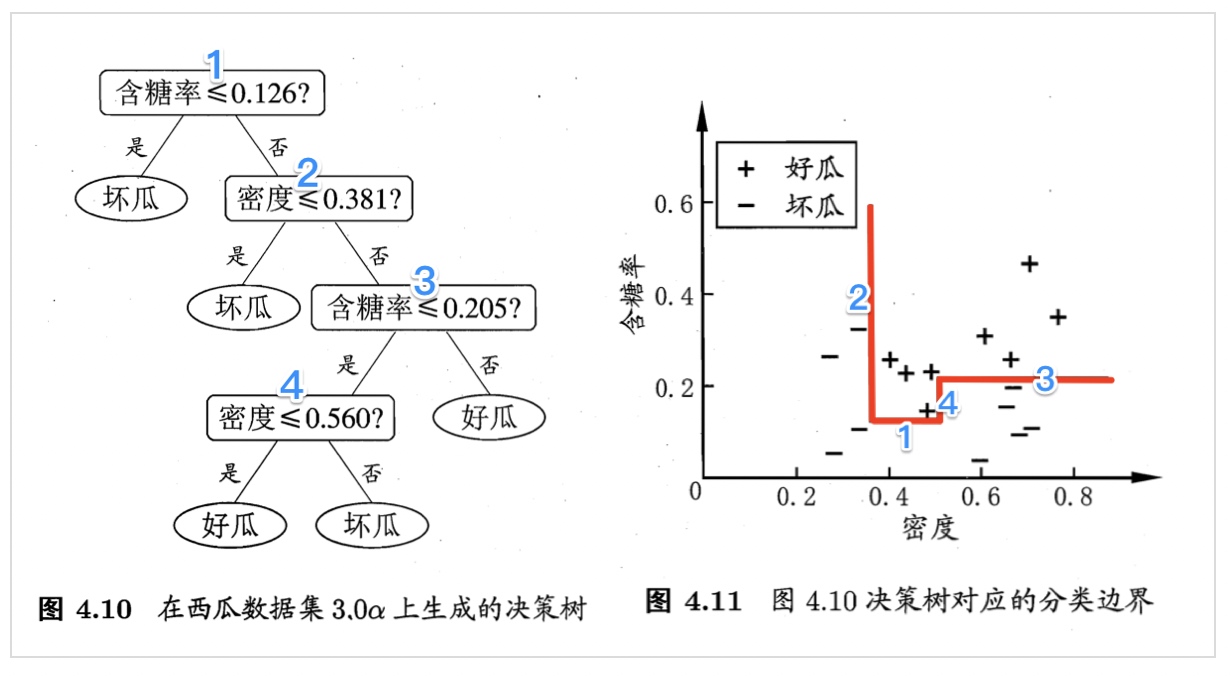
- 若使用“斜”的划分边界,如图4.12中的红色线段所示,则决策树模型将会大为简化。——“多变量决策树”multivariate decision tree 可以实现,甚至更复杂的划分。
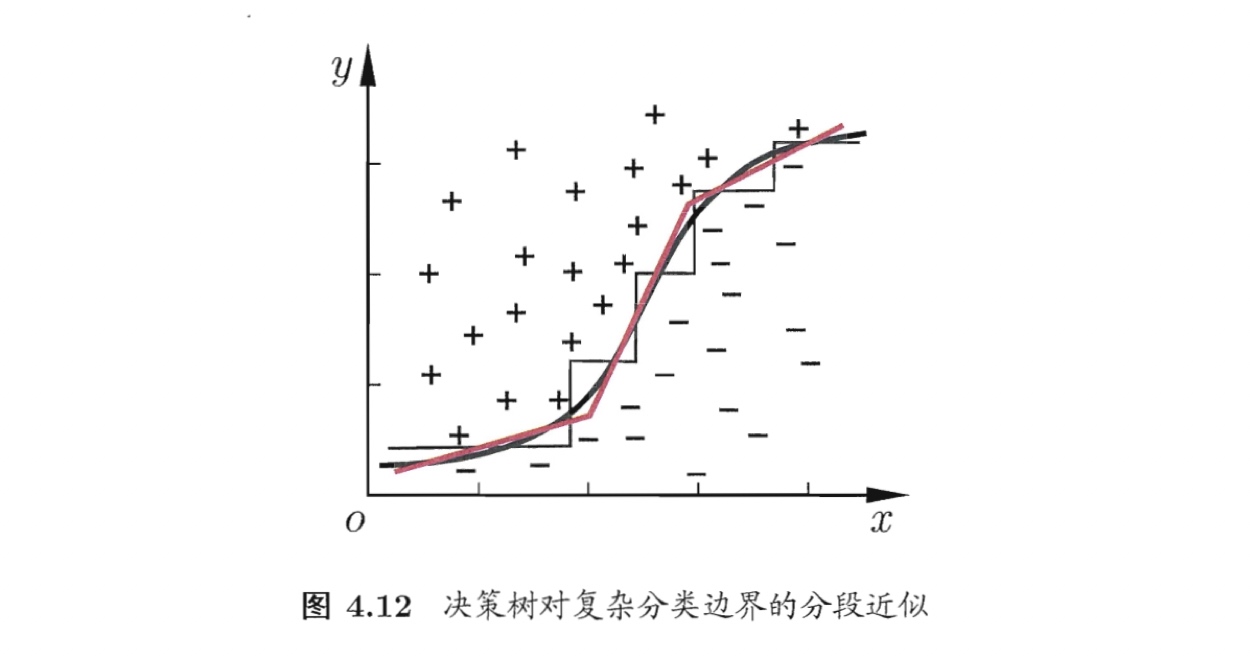
这样的多变量决策树亦称“斜决策树” oblique decision tree.
以实现斜划分的多变量决策树为例,在此类决策中,非叶结点不再是仅针对某个属性,而是对属性的线性组合进行测试;换言之,每个非叶节点是一个形如$\sum_{i=1}^d w_i a_i =t$的分类器,其中$w_i$是属性$a_i$的权重,$w_i$和$t$可在该结点所含样本集合属性集上学得。
与传统“单变量决策树”univariate decision tree不同,多变量决策树在学习过程中不是为每个非叶结点寻找一个最优划分属性,而是试图建立一个合适的线性分类器。
举一个例子🌰:
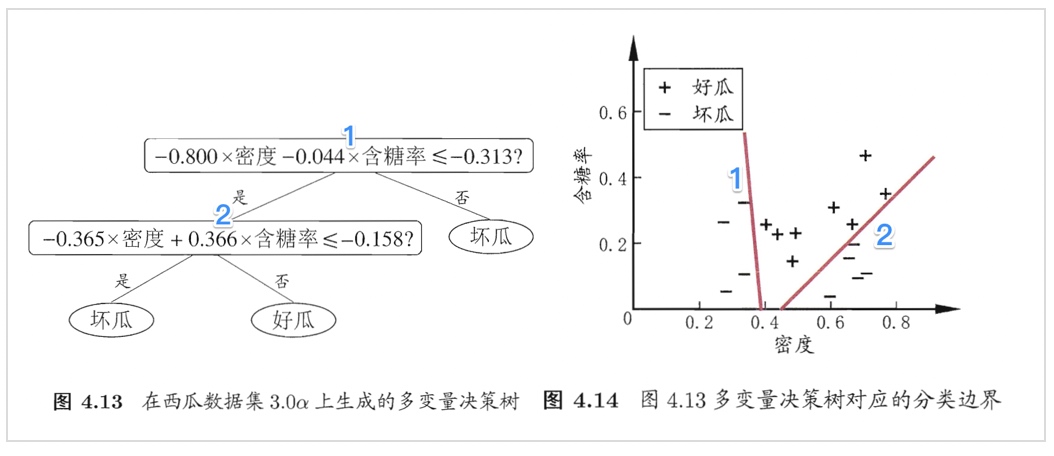
例如对西瓜数据3.0α,我们可学得图4.13这样的多变量决策树,其分类边界如图4.14所示。
Author Octemull
LastMod 2019-03-23