chap 03 - 线性模型 | Linear Model
Contents
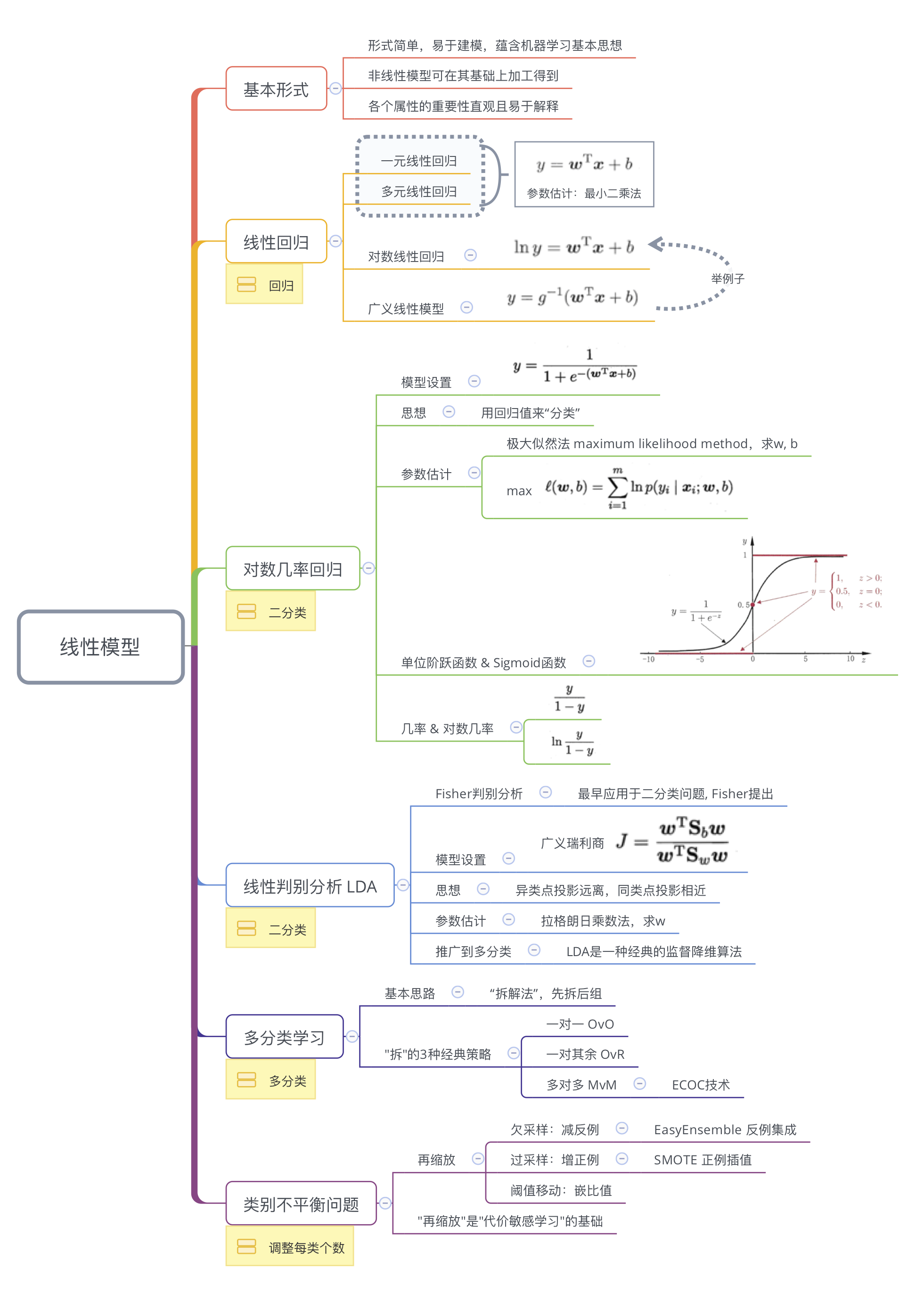
3.1 基本形式
给定由$d$个属性描述的样本$\boldsymbol{x}=(x_1,x_2,\cdots,x_d)^{\top}$,其中$x_i$是$\boldsymbol{x}$在第$i$个属性上的取值,线性模型视图习得一个通过属性的线性组合来进行预测的函数,即 $$f(\boldsymbol{x}) = w_1 x_1 + w_2 x_2 + \cdots + w_d x_d +b$$ 用向量形式表示为 $$f(\boldsymbol{x}) = \boldsymbol{w}^{\top} \boldsymbol{x} + \boldsymbol{b}$$ 其中,$\boldsymbol{w} = (w_1,w_2,\cdots, w_d)^{\top}$。模型由$ \boldsymbol{w}$和$ \boldsymbol{b}$确定。
特点:
- 形式简单,易于建模,但蕴含着机器学习中一些重要的基本思想;
- 许多功能强大的非线性模型(nonlinear model)可在线性模型的基础上引入层级结构或者高维映射得到;
- ω直观表示出各属性的重要性,易于解释(有很好的可解释性 comprehensibility)。
例子:若在西瓜问题中学得“f好瓜(x) = 0.2 • x色泽+ 0.5 • x根蒂+ 0.3 • x敲声+ 1”,则意味着可通过综合考虑色泽、根蒂和敲声来判断瓜好不好,其中根蒂最要紧,而敲声比 色泽更重要.
3.2 线性回归 linear regression
目的:
习得一个线性模型尽可能准确的预测实值输出标记,即 $f(\boldsymbol{x}_i) = \boldsymbol{w}^{\top} \boldsymbol{x}_i + \boldsymbol{b}$,使$f(\boldsymbol{x})_i \simeq y_i $
符号说明:
- 数据集 $D = {(\boldsymbol{x}_1,y_1), (\boldsymbol{x}_2,y_2), \cdots, (\boldsymbol{x}_m,y_m)}$.
- 样本 $\boldsymbol{x}_i = (x_{i1}; x_{i2}; \cdots; x_{id})$,每个样本有$d$个属性.
- 样本标记$y_i \in \mathbb{R}$.
3.2.1 一元线性回归
🔹模型构建:
- 符号: 输入属性的数目只有一个$(x_i)$时,$D = { (\boldsymbol{x}_1,y_1), (\boldsymbol{x}_2,y_2), \cdots, (\boldsymbol{x}_m. y_m) }$,其中$x_i \in \mathbb{R}$.
- 模型: $f(x_i) = w x_i + b$,使$f(x_i) \simeq y_i$
🔹参数估计:
方法:最小二乘法 least square method(“均方误差(MSE)最小化”)
待估参数:$w$,$b$
最小二乘法:找到一条直线,使所有样本到直线上的欧氏距离之和最小。
求解 $w, b$ , 使 $E_{(w,b)} = \sum_{i=1}^m (y_i - w x_i -b)^2$ 最小,可分别对 $w, b$ 求导.
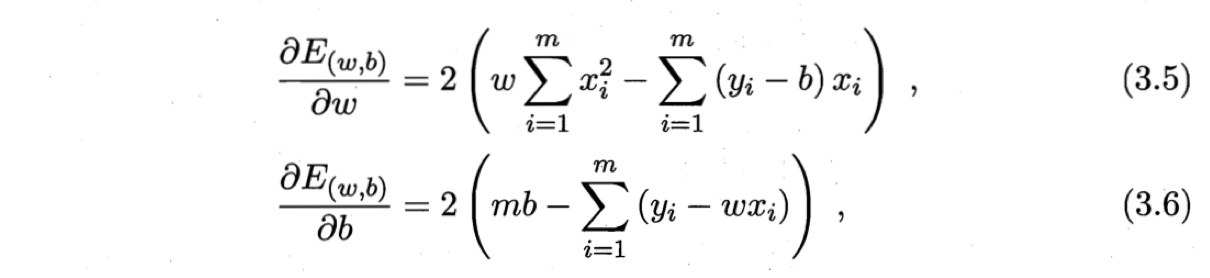 然后令两个式子等于零,即可得到$w$和$b$的最小二乘解。
然后令两个式子等于零,即可得到$w$和$b$的最小二乘解。
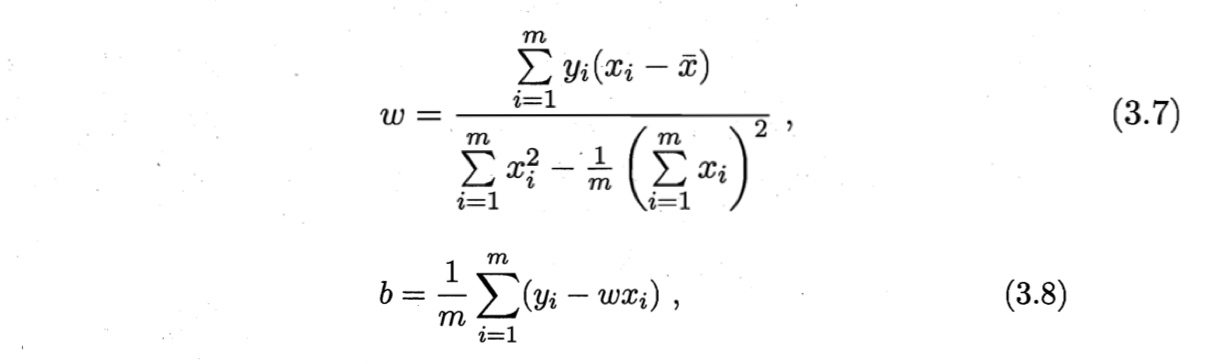
其中$\bar{x}=\frac{1}{m} \sum_{i=1}^m x_i$,是$x$的均值。
3.2.2 多元线性回归 multivariate linear regression
🔹模型构建:
- 符号:样本属性共$d$个,用$x_1, x_2, \cdots, x_d$表示;
- 模型:$f(\boldsymbol{x}_i) = \boldsymbol{w}^{\top} \boldsymbol{x}_i + \boldsymbol{b}$,使$f(\boldsymbol{x})_i \simeq y_i $
🔹参数估计: 方法:最小二乘法 least square method 待估参数:w、b
类似,用最小二乘法估计$w$和$b$。为了便于求解,将待估计参数写成向量形式$\hat{\boldsymbol{w}}=(\boldsymbol{w};b)$。用$\boldsymbol{X} \in \mathbf{R}^{m \times (d+1)}$表示数据集$D$,每行为一个样本,每列为一个属性,最后一列恒为1.
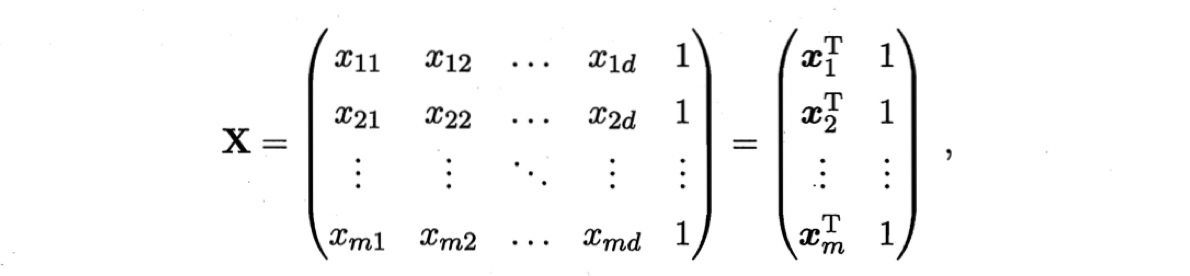
样本标记的向量为 $\boldsymbol{y} = (y_1;y_2;\cdots;ym)$ 。则最优化的目标函数为
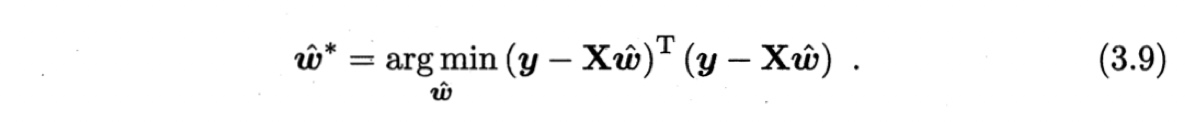 令$E{\hat{\boldsymbol{w}}} = (\boldsymbol{y} - \mathbf{X} \hat{\boldsymbol{w}})^{\top}(\boldsymbol{y} - \mathbf{X} \hat{\boldsymbol{w}})$,
令$E{\hat{\boldsymbol{w}}} = (\boldsymbol{y} - \mathbf{X} \hat{\boldsymbol{w}})^{\top}(\boldsymbol{y} - \mathbf{X} \hat{\boldsymbol{w}})$,
对$\hat{\boldsymbol{w}}$求导得
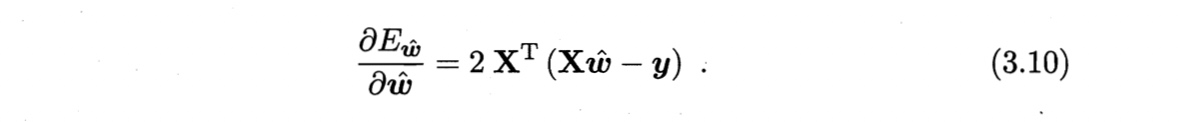
当$\mathbf{X}^T \mathbf{X}$满秩或正定时,令其等于0,得最优解为
$$\hat{\boldsymbol{w}}^{*} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \boldsymbol{y} $$
令$\hat{\boldsymbol{x}}_i = (\boldsymbol{x}_i;1)$,则最终学得的多元线性回归模型为
$$f(\hat{\boldsymbol{x}}_i) = \hat{\boldsymbol{x}}_i^T (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \boldsymbol{y}$$
但实际应用中,$\mathbf{X}^T \mathbf{X}$往往不是满秩的。如,变量数目超过样本数目。此时存在多个解。输出哪个解由学习算法的偏好决定,常见的做法是引入正则化项。
3.2.3 对数线性回归 log-linear regression 与 广义线性模型 generalized linear model
- 模型: $\ln y = \boldsymbol{w}^T \boldsymbol{x} +b$
- 特点:
- 引入非线性
- 实际模型为$y = \exp(\boldsymbol{w}^T \boldsymbol{x} +b)$
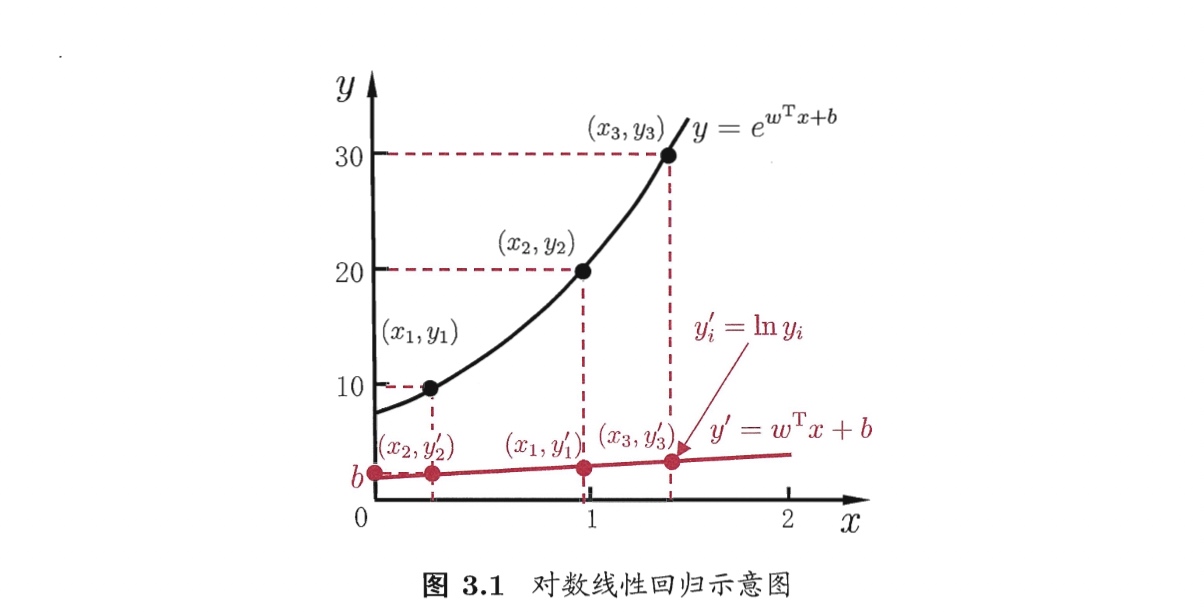
更一般的模型称为“广义线性模型”(generalized linear model): $$y = g^{-1}(\boldsymbol{w}^T \boldsymbol{x} +b)$$ 其中函数$g(\cdot)$称为“联系函数”(link function)。对数线性回归是当$g(\cdot)=ln(\cdot)$时的特例。
3.3 对数几率回归(对率回归)——“分类”方法
note
Q:什么是对数几率回归?
A:对数几率回归是一种分类学习的方法。以分两类为例进行说明。它把样本的属性值作为输入,经过回归,输出一个0到1之间的概率值。若该概率值大于某个特定值(称为“阈值”),则判断为正例;若小于,则判断该样本为反例。为了得到一个可以预测新样本类别的模型,可分为两步操作。
第一步,我们要用训练集中的样本训练出一个模型。我们知道:训练集样本中,标记1的为正例,标记0的为反例。那么怎么确定每个样本对应的概率值呢?通过“极大似然法”最大化对数似然函数,让每个样本属于真实标记的概率越大越好,如让正类样本的概率值接近1,反类样本的概率值接近0。
第二步,可以用“牛顿法”步步迭代,求出最大化对数似然函数问题的最优解。先任意取一组线性模型的参数值,记做β0,用所有训练样本的属性的函数值和标记带入迭代公式,得出β1;再用β1和训练样本数据迭代到β2……如此往复,直至β达到停止条件,就输出最终的模型参数值。常见的停止条件如连续两次的迭代结果的相对误差不大,绝对误差小于设定值等。如此,便得到了一个对数几率回归模型。
- 适用任务:分类(虽叫“回归”,但实际用于分类),每类数目相当
- 原理:基于广义线性模型,找一个单调可微函数将分类任务的真是标记y与线性回归模型的预测值联系起来。
- 具体方法:以二分类为例
🔹模型构建:
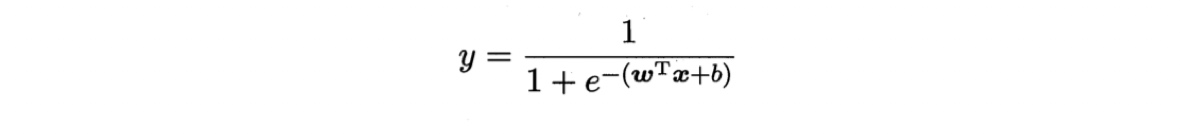
转换函数:
单位阶跃函数 unit-step function:单调,不连续,所以不可导。用于将线性模型产生的连续实输出值转化为0/1值的最理想函数。
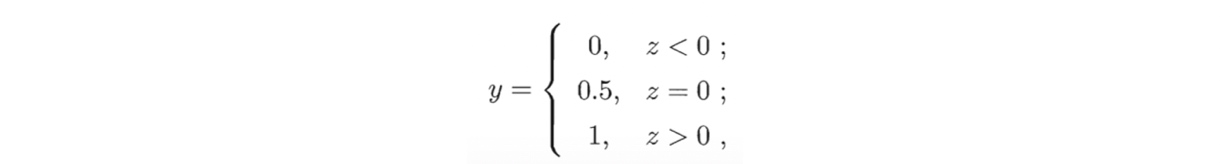
替代函数 surrogate function:因为单位阶跃函数不可导,无法用广义线性回归的公式,所以需找一个替代函数。常用“Sigmoid”函数。
对数几率函数 logistic function:单调连续且可微,且一定程度上近似单位阶跃函数。是单位阶跃函数的常用替代函数,是一种”Sigmoid”函数(将z值转化为一个接近0或1的y值,并且其输出值在z=0附近变化很陡,形似”S”)。 $$y = \frac{1}{1+e^{-z}}$$
推导广义线性模型
- 几率 odds:$\frac{y}{1-y}$,将y视为样本x作为正例的可能性,则1-y是其反例的可能性,两者比值称为几率,反映了x作为正例的相对可能性。
- 对数几率 log odds, logit:$\ln \frac{y}{1-y}$,几率取对数。
模型本质:用线性回归模型的预测结果去逼近真实标记的对数几率。
优点:
- 直接对分类可能性建模,无需实现假设数据分布,避免假设有误带来的误差;
- 不仅可以预测出“类别”,还可以得到近似“概率”,有利于概率辅助决策;
- 对数几率函数时任意阶可导的凸函数,具有良好的数学性质,有很多数值优化算法可直接用于求最优解。
例子:
考虑二分类任务,其输出标记$y\in {0,1}$,而线性回归模型产生的预测值$z = \boldsymbol{w}^T \boldsymbol{x} +b$是实数,需要转换为0/1. 最理想的转换函数为“单位阶跃函数”。若预测值$z>0$则判断为正例,小于0判断为反例,临界值任意判断。
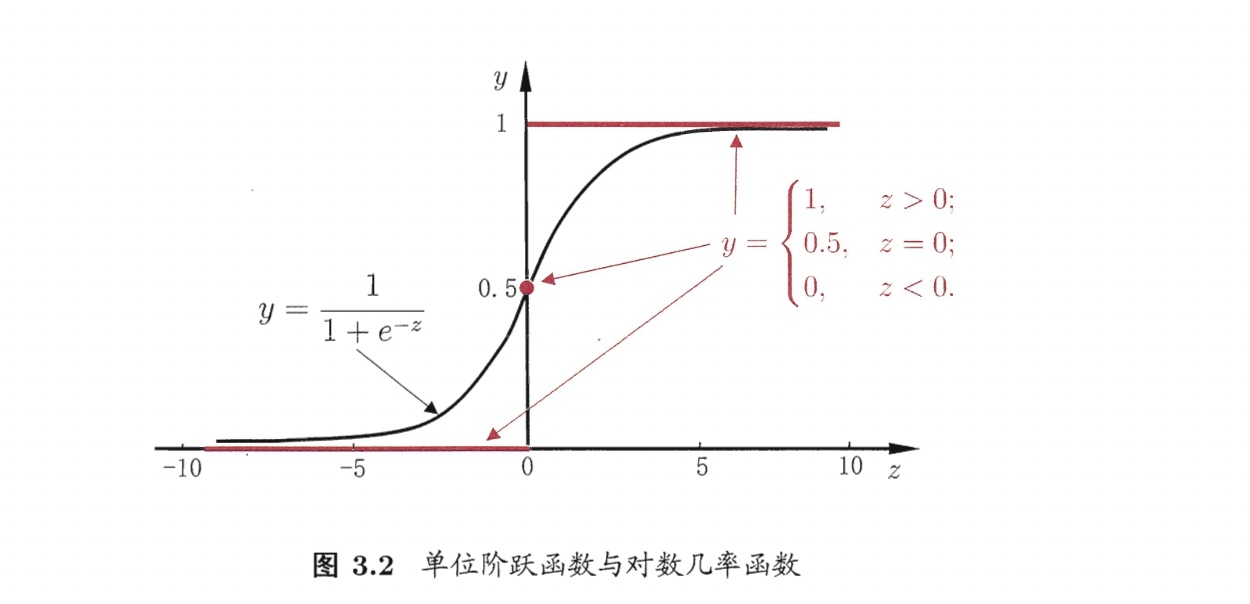 但是“单位阶跃函数”不连续,不好求逆函数。而logistic函数单调可微,它是一种”sigmoid”函数。sigmoid函数将实数集映射到0和1之间,且在$z=0$附近变化很陡。将logistic函数代入广义线性模型,可得
但是“单位阶跃函数”不连续,不好求逆函数。而logistic函数单调可微,它是一种”sigmoid”函数。sigmoid函数将实数集映射到0和1之间,且在$z=0$附近变化很陡。将logistic函数代入广义线性模型,可得
$$y = \frac{1}{1 + e^{-(\boldsymbol{w}^T \boldsymbol{x} +b)}}$$
可变形为
$$\ln \frac{y}{1-y} = \boldsymbol{w}^T \boldsymbol{x} +b$$
logistic函数做转换函数即用线性回归$\boldsymbol{w}^T \boldsymbol{x} +b$逼近$\ln \frac{y}{1-y}$,是一种广义线性回归。
🔹参数估计
方法: 极大似然法 maximum likelihood method
待估参数: $w,b$
概率的归一性
$p(y=1|x)+p(y=0|x)=1$
推导:
将$y$视为类后验概率估计$p(y=1|\boldsymbol{x})$,则有
$$\ln \frac{p(y=1|\boldsymbol{x})}{p(y=0|\boldsymbol{x})} = \boldsymbol{w}^T \boldsymbol{x} +b$$
由概率的归一性可得
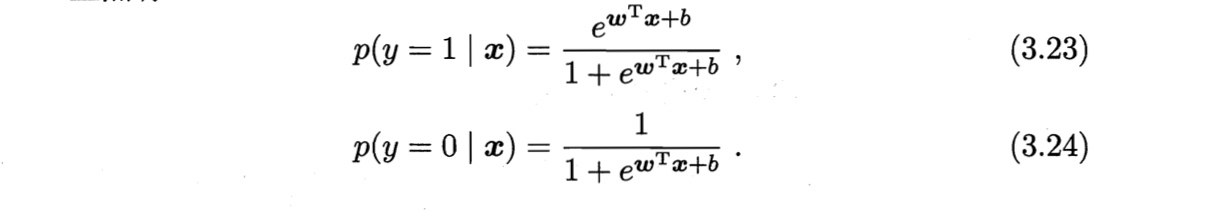
根据“极大似然法”,给定数据集为${(\boldsymbol{x}_i, yi)}{i=1}^m$,最大化回归模型的似然函数
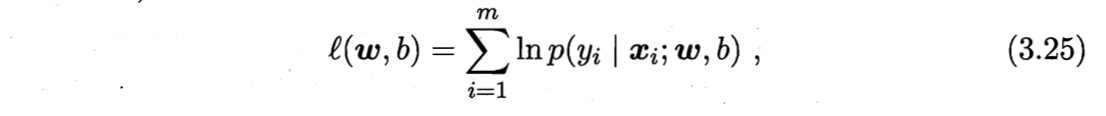
即,令每个样本属于其真实标记的概率越大越好。为了便于讨论,令$\boldsymbol{\beta} = (\boldsymbol{w};b)$,$\hat{\boldsymbol{x}} = (\boldsymbol{x};1)$,则$\boldsymbol{w}^T \boldsymbol{x} +b$可以简写为$\boldsymbol{\beta}^T \hat{\boldsymbol{x}}$。再令$p_1(\hat{\boldsymbol{x}};\boldsymbol{\beta})= p(y=0|\hat{\boldsymbol{x}};\boldsymbol{\beta})=1-p_0(\hat{\boldsymbol{x}};\boldsymbol{\beta})$ 。则似然项可重写为
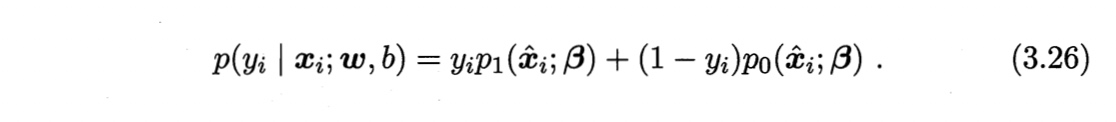
则最大化似然函数等价于最小化下式
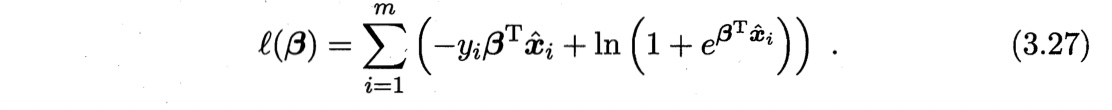
根据凸优化理论,采用梯度下降法、牛顿法都可求得其最优解
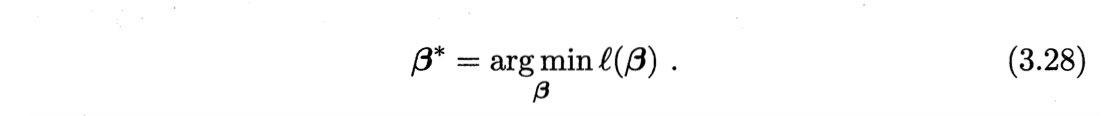
以牛顿法为例
$t+1$轮的迭代解的更新公式为
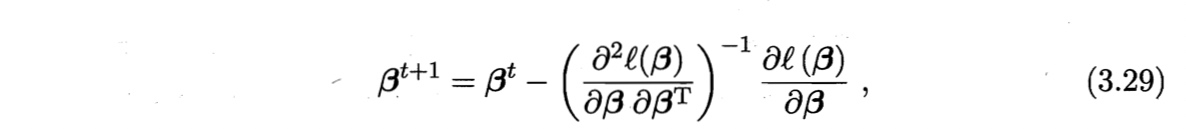
其中关于$\boldsymbol{\beta}$的一阶、二阶倒数分别为
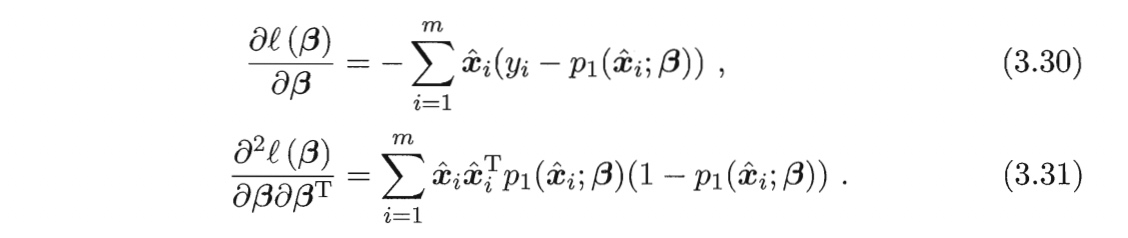
3.4 线性判别分析 Linear Discriminant Analysis, LDA
别名: 在“二分类”问题上最早由Fisher提出,亦称“Fisher判别分析”。(严格说二者稍有不同,LDA假设了个样本的协方差矩阵相同且满秩。)
适用任务: 分类,每类数目相当
思想: 使异类点投影远离,同类点投影相近
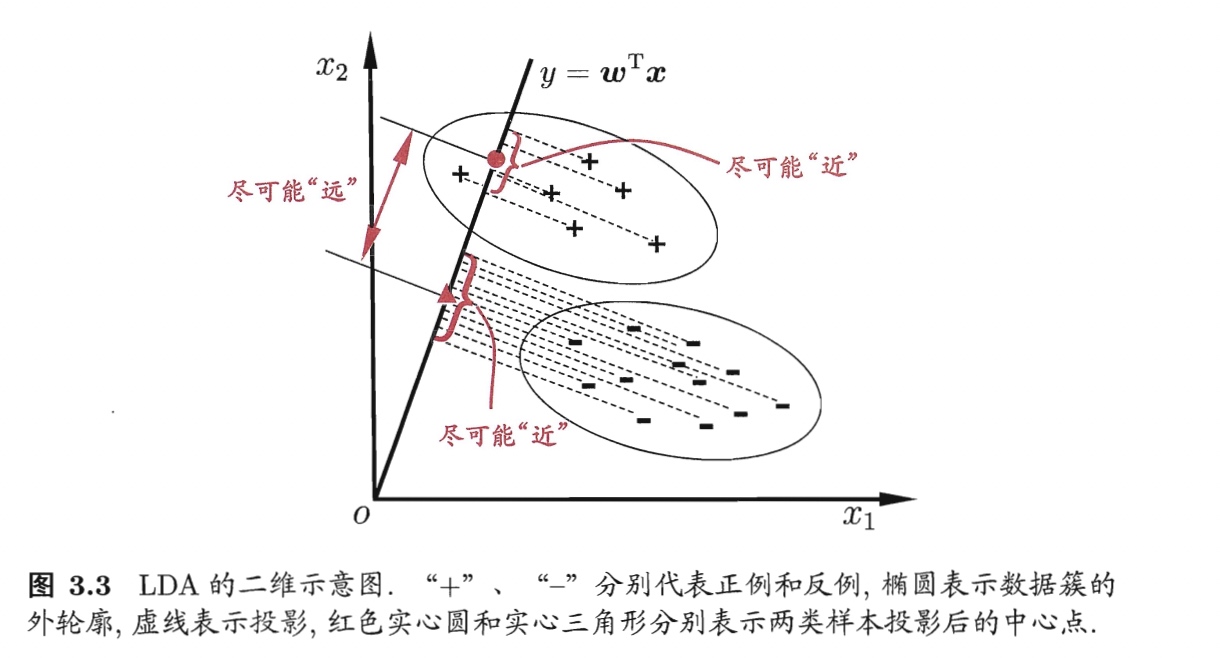
🔹模型构建:以“二分类”为例
概念:
- 示例集合、均值向量、协方差矩阵,第i类表示为:$X_i,\ \boldsymbol{\mu}_i, \ \boldsymbol{\Sigma}_i$
类内散度矩阵 within-class scatter matrix、类间散度矩阵 between-class scatter matrix:
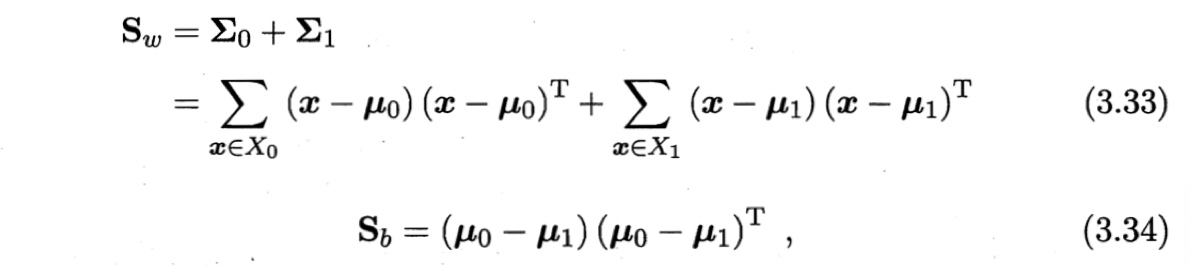
广义瑞利商 generalized Rayleigh quotient:
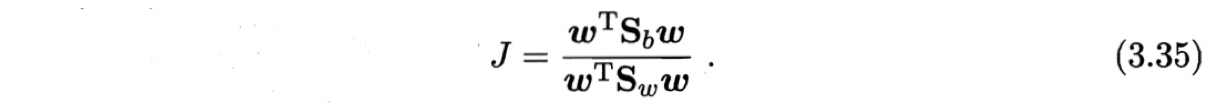
目标:
要使同类样例投影尽可能近,可以使同类投影点的协方差尽可能小;要使异类的远,则使其协方差大。若将数据投影到直线$\boldsymbol{w}$上,则两类样本的中心再直线上的投影分别为$\boldsymbol{w}^T \boldsymbol{\mu}_0$和$\boldsymbol{w}^T \boldsymbol{\mu}_1$;协方差为$\boldsymbol{w}^T \boldsymbol{\Sigma}_0 \boldsymbol{w}$和$\boldsymbol{w}^T \boldsymbol{\Sigma}_1 \boldsymbol{w}$。由于直线是一维的,所以上述投影和方差均为实数。
因此,最大化目标为
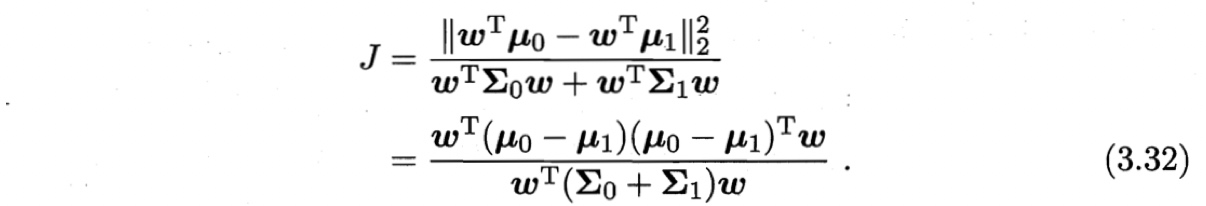
用类内散度矩阵、类间散度矩阵可表示为广义瑞利商。
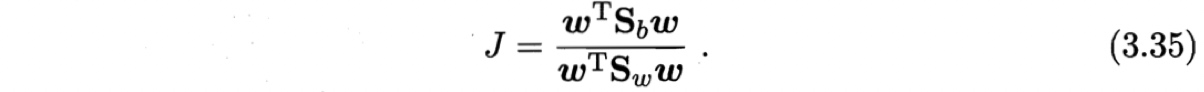
🔹参数估计: $\boldsymbol{w}$
若$\boldsymbol{w}$是一个解,则$a\boldsymbol{w}$也是一个解。说明(3.35)的解与$\boldsymbol{w}$的长度无关,只与其方向有关。令$\boldsymbol{w}^T \boldsymbol{S}_w \boldsymbol{w}=1$,则优化问题为
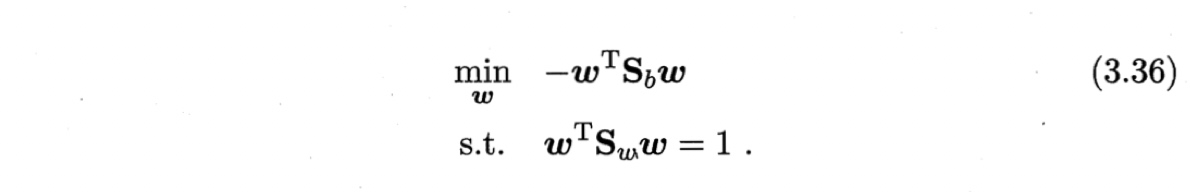
由拉格朗日乘子法,上式等价于
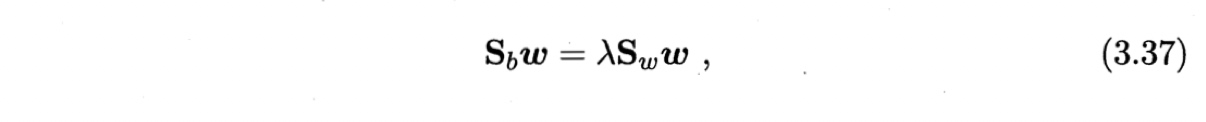
其中$\lambda$是拉格朗日乘子。注意到$\boldsymbol{S}_b\boldsymbol{w}$的方向恒为$\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1$,不妨令
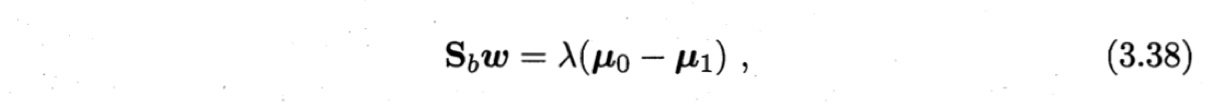
代入(3.37)即得
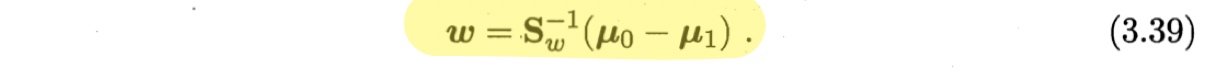
考虑到数值解的稳定性,在实践中通常对$\boldsymbol{S}_w$进行奇异值分解,即$\boldsymbol{S}_w = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^T$,其中$\boldsymbol{\Sigma}$是一个实对角矩阵,其对角线上的元素是$\boldsymbol{S}_w$的奇异值,然后再由$\boldsymbol{S}_w^{-1} = \boldsymbol{V} \boldsymbol{\Sigma}^{-1} \boldsymbol{U}^T$得到$\boldsymbol{S}_w^{-1}$。
🔸LDA可从贝叶斯决策理论的角度来解释,并可证明,当两类数据同先验、满足高斯分布且协方差相等时,LDA可达到最优分类。
🔹模型推广:“多分类”
假定存在$N$个类,且第$i$类示例数为$m_i$。定义“全局散度矩阵”
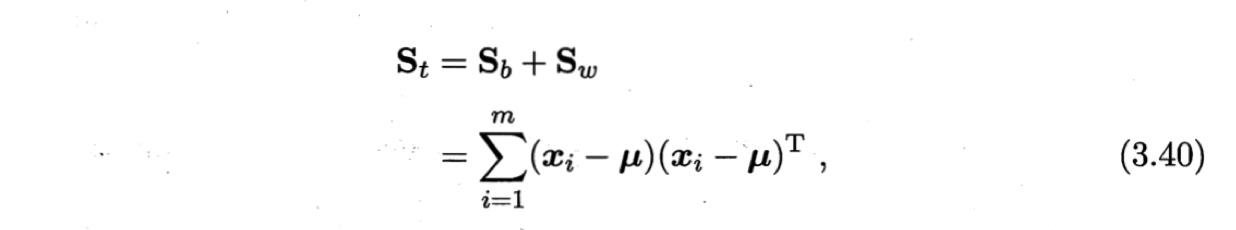
其中$\boldsymbol{\mu}$是所有示例的均值向量。将“类内散度矩阵”$\boldsymbol{S}_w$重定义为每个类别的散度之和
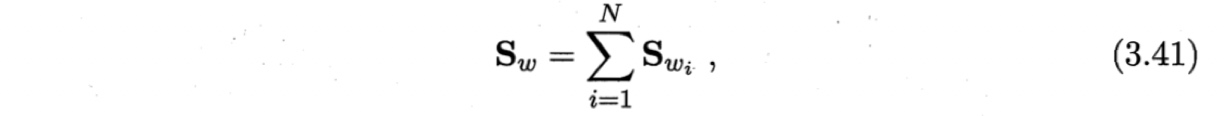
其中
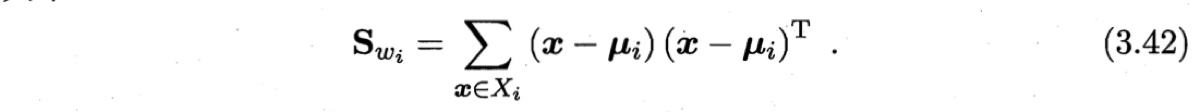
由式(3.40)~(3.42)可得
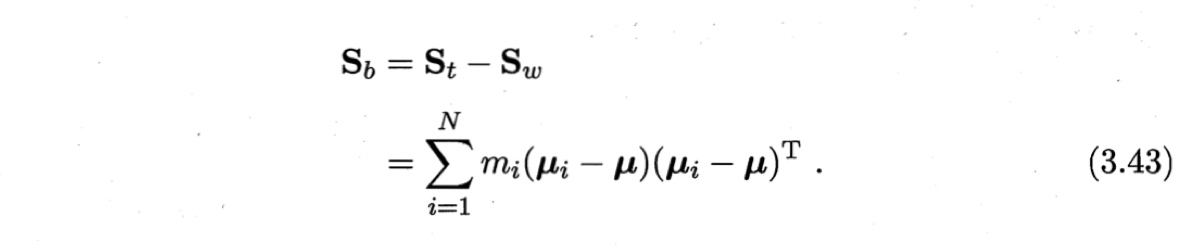
可见,多分类的LDA有多种实现方法:使用$\boldsymbol{S}_b, \ \boldsymbol{S}_w, \ \boldsymbol{S}_t$三者中的任何两个即可。常见的一种是采用优化目标
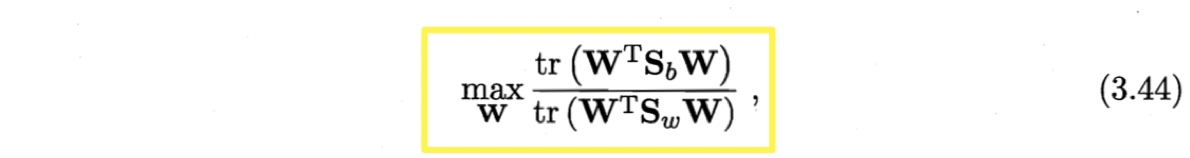
其中$\mathbf{W} \in \mathbb{R}^{d\times (N-1)}$,$tr(\cdot)$表示矩阵的迹(trace).上式通过如下广义特征问题求解:
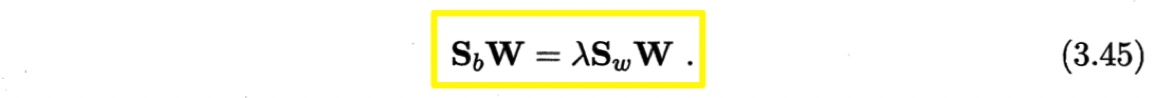 $\mathbf{W}$的闭式解为$\boldsymbol{S}_w^{-1}\boldsymbol{S}_b$的$d’$个最大非零广义特征值所对应的特征向量组成的矩阵,$d’ \leq N-1$(最多有$N-1$个非零特征值)。
$\mathbf{W}$的闭式解为$\boldsymbol{S}_w^{-1}\boldsymbol{S}_b$的$d’$个最大非零广义特征值所对应的特征向量组成的矩阵,$d’ \leq N-1$(最多有$N-1$个非零特征值)。
若将$\mathbf{W}$视为一个投影矩阵,则多分类LDA将样本投影到$d’$维空间,$d’$通常远小于数据原有的属性个数。因此,可通过投影减少样本的维数,LDA也被视为一种经典的监督降维技术。
3.5 多分类学习
适用问题: 分类,每类数目相当
基本思路: “拆解法”,即将多分类任务拆解为若干个二分类任务求解。(有的二分类算法可推广至多分类,如,LDA)。具体来说,先对问题进行拆分,然后为拆出的每个二分类任务训练一个分类器;在测试时,对这些分类器的预测结果进行集成以获得最终的多分类结果。 关键:如何拆?怎么组?(如何拆分多分类任务?如何集成多个分类器?)
如何拆?三种经典策略:
- 一对一 (One vs. One, OvO)
- 一对其余 (One vs. Rest, OvR)
- 多对多(Many vs. Many, MvM)
三者关系:
OvO与OvR
- OvO的存储开销和测试时间通常大于OvR(OvO训练N(N-1)/2个分类器,OvR只训练N个);
- 类别多时,OvO的训练时间开销往往小于OvR(OvR的每个分类器使用全部数据,OvO只使用两个类别的数据);
- 预测性能取决于具体数据分布,多数情况下两者差不多。
MvM与OvO、OvR
- OvO和OvR是MvM的特殊情况。
- OvO和OvR是MvM的特殊情况。
符号:
给定数据集$D = {(\boldsymbol{x}_1,y_1), (\boldsymbol{x}_2,y_2), \cdots, (\boldsymbol{x}_m. y_m)}, \ y_i \in {C_1, C_2, \cdots, C_N}$
1️⃣一对一 (One vs. One, OvO)
将N个类别两两配对,从而产生N(N-1)/2个二分类任务。
如,OvO将为区分类别C_i和C_j训练一个分类器,该分类器把D中的C_i类样例作为正例,C_j类样例作为反例。在测试阶段,新样本将同时提交给所有分类器,于是得到N(N-1)/2个分类结果,最终结果可通过投票产生:即把被预测得最多的类别作为最终分类结果。图3.4给出了一个示意图。
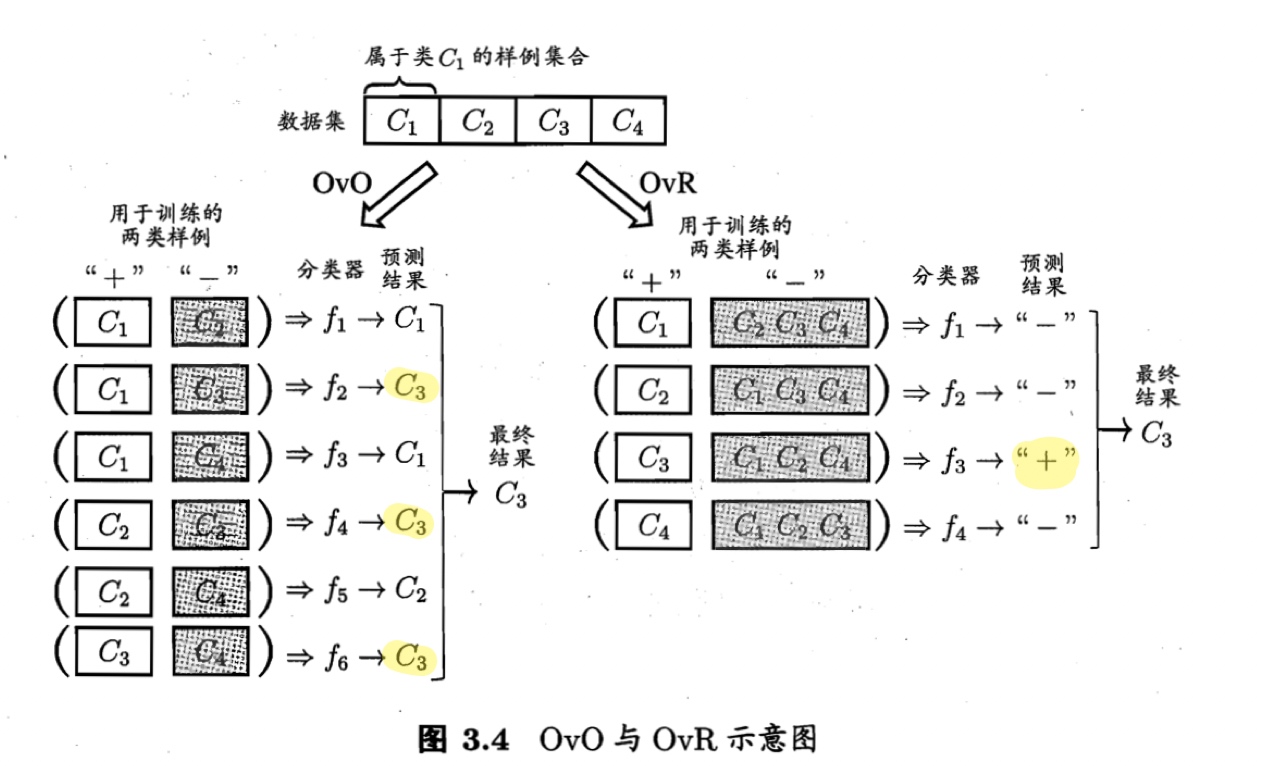
2️⃣一对其余 (One vs. Rest, OvR)
每次将一个类的样例作为正例、所有其他类的样例作为反例来训练N个分类器。
在测试时,若仅有一个分类器预测为正类,则对应的类别标记作为最终分类结果,如图3.4;若有多个分类器预测为正类,则通常考虑各分类器的预测置信度,选择置信度最大的类别标记作为分类结果。
3️⃣多对多(Many vs. Many, MvM)
每次将若干个类作为正类,若干个其他类作为反类。MvM的正、反类必须采取特殊设计,不能随意选取,最常用的MvM技术为“纠错输出码”(Error Correcting Output Codes, ECOC)。
ECOC[Dietterich and Bakiri, 1995]是将编码的思想引入类别拆分,并尽可能在解码过程中具有容错性。
ECOC步骤:
- 编码:对N个类别做M次划分,每次划分将一部分类别划为正类,一部分划为反类,从而形成一个二分类训练集;一共产生M个训练集,可训练M个分类器。
- 解码:用M个分类器分别对样本进行预测,这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为最终预测结果。
类别划分通过“编码矩阵”(coding matirx)指定。编码矩阵的常见形式主要有:
- 二元码:将每个类别分别指定为正类、反类。
- 三元码:除正、反类之外,还可指定“停用类”。
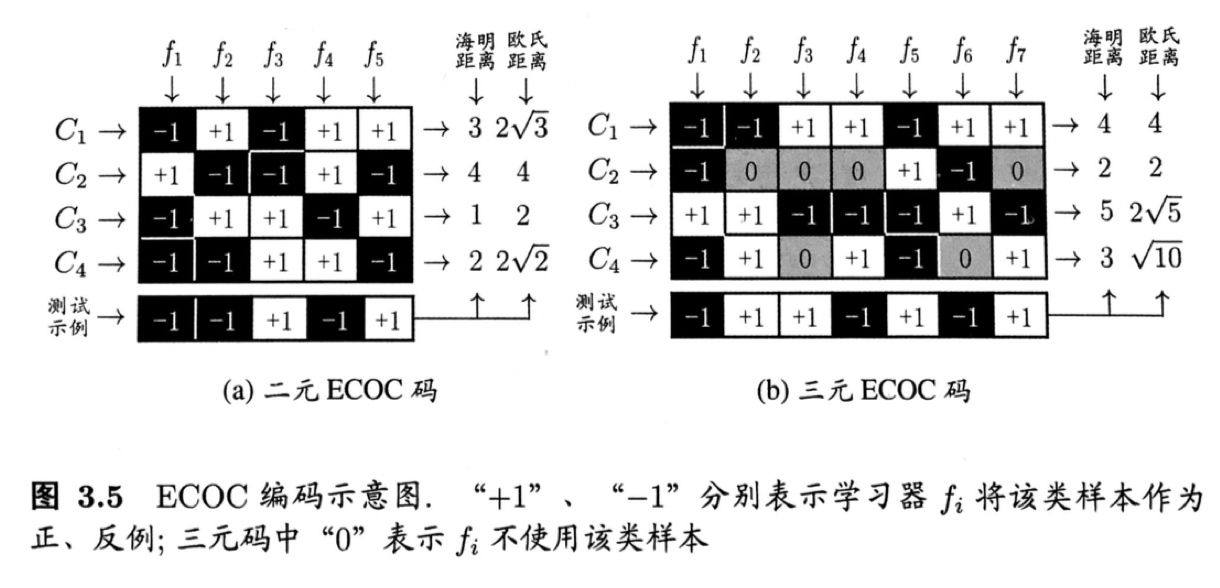
如,图3.5(a)中,分类器f2将C1类和C3类的样例作为正例,C2类和C4类的样例作为反例;图3.5(b)中,分类器f4将C1、C4类作为正例,C3作为反例。 在解码阶段,各分类器的预测结果联合起来形成测试示例的编码,与各类样例的编码比较,取距离最小的编码对应的类别作为预测结果。 如,图3.5(a)中,若基于欧式距离,则预测结果为C3。
ECOC的“纠错”特性:
- 在测试阶段,ECOC编码对分类器的错误具有一定的容忍和修正能力。
- 一般,对同一任务而言,ECOC编码越长,纠错能力越强。(但编码越长,计算开销越大;另外,对有限类别数,可能的组合数目是有限的,码长超过一定范围后就失去了意义。)
- 理论上,同等长度的编码,任意两个类别之间的编码距离越远,则纠错能力越强。(码长较小时,可根据此原则计算出理论最优编码。)
纠错的例子:
如,在图3.5(a)中对测试示例的正确预测编码为(-1, +1, +1, -1, +1),假设预测时某个分类器出错了,例如f2出错导致错误编码(-1, -1, +1, -1, +1),但基于这个编码仍然可以产生正确的最终分类结果C3.
不过,
通常我们并不需获得理论最优编码,因为非最优编码在实践中往往已能产生足够好的分类器.另一方面,并不是编码的理论性质越好,分类性能就越好,因为机器学习问题涉及很多因素,例如将多个类拆解为两个“类别子集”,不同拆解方式所形成的两个类别子集的区分难度往往不同,即其导致的二分类问题的难度不同;于是,一个理论纠错性质很好、但导致的二分类问题较难的编码,与另一个理论纠错性质差一些、但导致的二分类问题较简单的编码,最终产生的模型性能孰强孰弱很难说.
3.6 类别不平衡问题 class-imbalance
适用任务: 分类任务中,每类数目差异大
如,{998-, 2+}的数据集,学习器只要返回一个永远将新样本预测为反例的学习器,就能达到99.8%的精度。但是这样的学习器往往没有价值,因为它不能预测出任何正例。
如,用拆分法解决多分类问题时,即使原始问题中类别均衡,在使用OvR、MvM策略后产生的二分类任务仍可出现类别不平衡现象。(对OvR、MvM来说,由于对每个类进行了相同的处理,其拆接触的二分类任务中类别不平衡的影响会互相抵消,因此通常不需专门处理。)
基本策略: 再缩放 rescaling / 再平衡 rebalance
以线性分类器为例:
在我们用$y=w^Tx+b$对新样本$x$进行分类时,事实上是在用预测出的$y$值与一个阈值进行比较,例如通常在$y>O.5$时判别为正例,否则为反例. $y$实际上表达了正例的可能性,几率$\frac{y}{1-y}$则反映了正例可能性与反例可能性之比值,阈值设置为$0.5$恰表明分类器认为真实正、反例可能性相同,即分类器决策规则为
若$\frac{y}{1-y}>1$则 预测为正例 (3.46)
然而,当训练集中正反例的数目不同时,令$m^+$表示正例数目,$m^-$表示反例数目,则观测几率是$\frac{m^+}{m^-}$,由于我们通常假设训练集是真实样本总体的无偏采样,因此观测几率就代表了真实几率.于是,只要分类器的预测几率高于观测几率就应判定为正例,即
若$\frac{y}{1-y}>\frac{m^+}{m^-}$则 预测为正例 (3.47)
但是,我们的分类器是基于式(3.46)进行决策,因此,需对其预测值进行调整,使其在基于式(3.46)决策时,实际是在执行式(3.47). 要做到这一点很容易,只需令
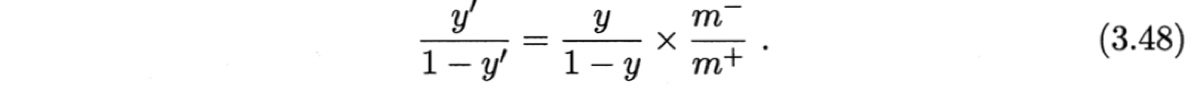
“再缩放”策略的难点:
假设“训练集是真是样本总体的无偏采样”往往不成立,即,我们未必能有效地基于训练集观测几率来推断出真实几率。
解决方法:(假设反例多于正例)
- 欠采样 undersampling / 下采样 downsampling:对训练集里的反类样例欠采样,即去除一些反例使正、反例数目接近,然后再进行学习;
- 过采样 oversampling / 上采样 upsampling:对训练集里的正类样例过采样,即增加一些正例使正、反例数目接近,然后再进行学习;
- 阈值移动 threshold-moving:直接基于原始训练集进行学习,但在用训练好的分类器进行预测时,将式(3.48)嵌入到决策过程中。
注意
- 通常,欠采样时间开销<<过采样(前者丢弃样例使训练集减小,后者增加样例使训练集增大)。
- 过采样不能简单地对原始样本重复采样,会导致过拟合(SMOTE [Chawla et al., 2002]通过对训练集里的正例插值得到新的正例样本);
- 欠采样若随机丢弃样例,可能丢失重要信息(EasyEnsemble [Liu et al., 2009]利用集成学习机制,将反例划分为若干个不同集合供不同学习器使用,总体上未丢失信息,但对每个学习器都进行了欠采样)。
MORE:
“再缩放”是“代价敏感学习”(cost-sensitive learning)的基础。将(3.48)式中的m-/m+换成cost+/cost-,即得代价敏感学习的表示,其中cost+是将正例误分为反例的代价,cost-是将反例误分为正例的代价。
Author Octemull
LastMod 2019-03-17