chap 01 - 绪论
Contents
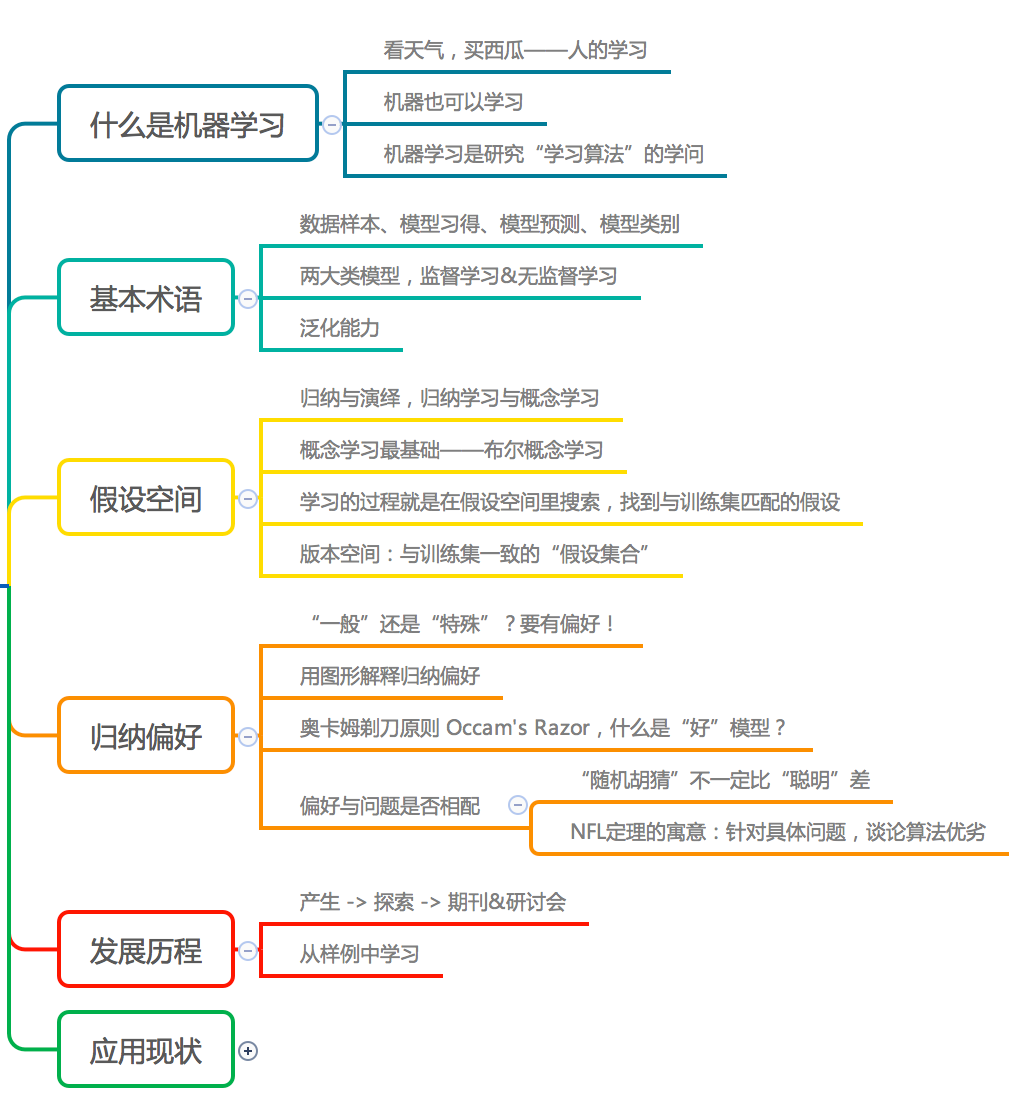
1.1 引言——什么是“机器学习”(machine learning)
- 走在街上看天气、买西瓜的一天 —— 我们根据自己的经验对未知的事情做出了预测或判断
- 机器学习——将信息输入机器,由机器产生模型,从而对未知的事情做出预判
- 机器学习是研究“学习算法”的学问
1.2 基本术语
关于数据样本
- 数据集 data set:一组描述不同个体的各种属性信息的集合
- 示例 instance / 样本 sample:一个个体、事件、对象。如,一个西瓜,一个机场。
- 属性 attribute / 特征 feature:反映事件或对象在某方面的表现或者性质的事项。如,色泽,敲声,是否成熟。
- 属性值 attribute value:属性的取值。如,颜色——红、黄、蓝…
- 属性空间 attribute space / 样本空间 sample space / 输入空间:属性张成的空间。如,把西瓜的“色泽”“根蒂”“敲声”作为三个坐标轴,则它们张成一个用于描述西瓜的三维空间。
- 特征向量 feature vector:示例在属性空间中的另一种叫法。续上,在该三维空间中,每个西瓜都可以用一个向量表示,空间中每一个点都对应一个向量坐标,即“特征向量”。
- 维数 dimensionality:在某数据集中,一个对象的属性的个数。续上上,西瓜数据集的维数 = 3,因为有三个不同的属性。
关于模型习得
- 学习 learning / 训练 training:从数据中学习,通过某种算法得到模型的过程。如,从西瓜的特征里学习,得到预测西瓜是不是好瓜的模型。
- 训练数据 training data:输入进机器,用来得到模型的数据。如上,一些西瓜的“色泽”“根蒂”“敲声”属性及其取值。
- 训练样本 training sample:训练数据中的每一个样本。如上,每一个西瓜都是一个训练样本。
- 训练集 training set:训练样本组成的集合。如上,一堆西瓜。
- 假设 hypothesis:学得模型对应了关于数据的某种潜在规律。如,学得的模型可以通过西瓜的某些特征,判断西瓜是不是好瓜。
- 真相/真实 ground-truth:续上,事物的潜在规律本身。如,好瓜的真实规律。
- 学习器 learner:习得的模型的另一称呼。
关于预测 ( prediction )模型
- 标记 label:关于示例结果的信息。如上,“好瓜”就是一个标记。
- 样例 example:有标记的示例。如,(色泽 = 青绿;根蒂 = 蜷缩;敲声 = 浊响)为一个示例,((色泽 = 青绿;根蒂 = 蜷缩;敲声 = 浊响),好瓜)为一个样例。一般,用$(\boldsymbol{x}_i, y_i)$表示第$i$个样本,其中$y_i \in \mathcal{Y}$是示例$\boldsymbol{x}_i$的标记,$\mathcal{Y}$是所有标记的集合,也叫“标记空间”(label space)或“输出空间”。
关于不同类型的学习任务
- 分类 classification:预测离散值。如,“好瓜”、“坏瓜”。
- 二分类任务 binary classification:标记只有两个取值。称其中一类为“正类” positive class,另一类为“反类” negative class。
- 多分类任务 multi-class classification:有多个类别。
- 回归 regression:预测连续值。如,西瓜的成熟度0.95、0.37。
一般的,预测任务是希望通过对训练集${(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2), \cdots, (\boldsymbol{x}_m,y_m)}$进行学习,建立一个从输入空间$\mathcal{X}$到输出空间$\mathcal{Y}$的映射$f: \mathcal{X} \rightarrow \mathcal{Y} $. - 对于二分类任务,通常令$\mathcal{Y}={-1,+1}$或${0,1}$; - 对多分类任务,$| \mathcal{Y}| >2$; - 对于回归任务,$\mathcal{Y} =\mathbb{R}$,$\mathbb{R}$为实数集。
习得模型后,用气进行预测的过程称为“测试”(testing),被预测的样本成为“测试样本”(testing sample)。例如,在学得$f$后,对测试例$\boldsymbol{x}$,可得到其预测标记为$f(\boldsymbol{x}_i)$。
- 聚类 clustering:将训练集中的样本自动分成若干组,每组可能暗含某种内在的、事先不知道的规律。如,把西瓜聚类,可能出现“浅色瓜”“深色瓜”,“本地瓜”“外地瓜”等。
两大类模型
- 监督学习 supervised learning:有标记信息。如,分类、回归。
- 无监督学习 unsupervised learning:无标记信息。如,聚类。
学习目的——泛化能力 generalization
- 使习得的模型能较好的预测“新样本”,而不是老样本(训练样本)。
- 训练集是小空间(整个空间的一小部分),希望模型在整个空间上仍有好的表现。
- 一般而言,样本越多,越容易得到泛化能力强的模型
⭐️假设 * 样本空间中全体样本服从一个未知的“分布” distribution * 每个样本都是独立从这个分布上采样获得的,即独立同分布 independent and identically distributed, i.d.d.
1.3 假设空间
归纳与演绎,归纳学习与概念学习
科学推理的两大基本手段是 归纳 induction 与 演绎 deduction 。前者是从特殊到一般的“泛化” generalization 过程(从具体事实推导出一般性的规律),后者是从一般到特殊的“特化” specialization 过程(从基础原理推导出具体状况)。 归纳学习有狭义、广义之分。广义的归纳学习大致指从样例中学习,狭义的则要求从训练数据中学得概念 concept,亦称“概念学习”或“概念形成”。概念学习对泛化的要求太高,目前的研究不足,现实中大多是“黑箱”模型。但对其有一定的了解,有助于我们理解机器学习的一些基础思想。
概念学习最基础——布尔概念学习
布尔概念学习即对“是”与“不是”此类可表示为0/1布尔值的目标概念的学习。举一个🌰,假定我们获得了如下一个训练集:
 我们的学习目标是“好瓜”。假设表中所给“色泽”“根蒂”“敲声”三个属性能完全决定一个瓜是不是好瓜,即“什么色泽,什么根蒂,什么敲声的瓜是好瓜?”用布尔表达式表示,如下:
我们的学习目标是“好瓜”。假设表中所给“色泽”“根蒂”“敲声”三个属性能完全决定一个瓜是不是好瓜,即“什么色泽,什么根蒂,什么敲声的瓜是好瓜?”用布尔表达式表示,如下:
好瓜 ⟷ ( 色泽 = ?)∧( 根蒂 = ?)∧( 敲声 = ?)
我们学习的任务就是把“ ?”给定下来。不是仅仅记住样例,还要能泛化。
学习的过程:在假设空间里搜索,找到与训练集匹配( fit )的假设
假设假设空间由形如“( 色泽 = ?)∧( 根蒂 = ?)∧( 敲声 = ?)”的可能取值的假设构成(假设:一个样本的属性的可能取值的表示)。如,“色泽”可取“青绿”“乌黑”“浅白”,其他的用通配符“ ∗ ”代替(也许“色泽”取什么值都合适)。同时考虑对标记的假设,标记为“好瓜”“坏瓜”;考虑极端情况(假设不存在或错误),若世界上没有“好瓜”这种东西,则用“∅”表示。 假设的表示一旦确定,假设空间的大小也就确定了。
例子,若“色泽” “根蒂” “敲声”分别有3、2、2种可能取值,则我们面临的假期空间规模大小为$4 \times 4 \times 4 + 1 = 65$ (“1”指“∅”)。下图直观展示了这个西瓜问题的假设空间。
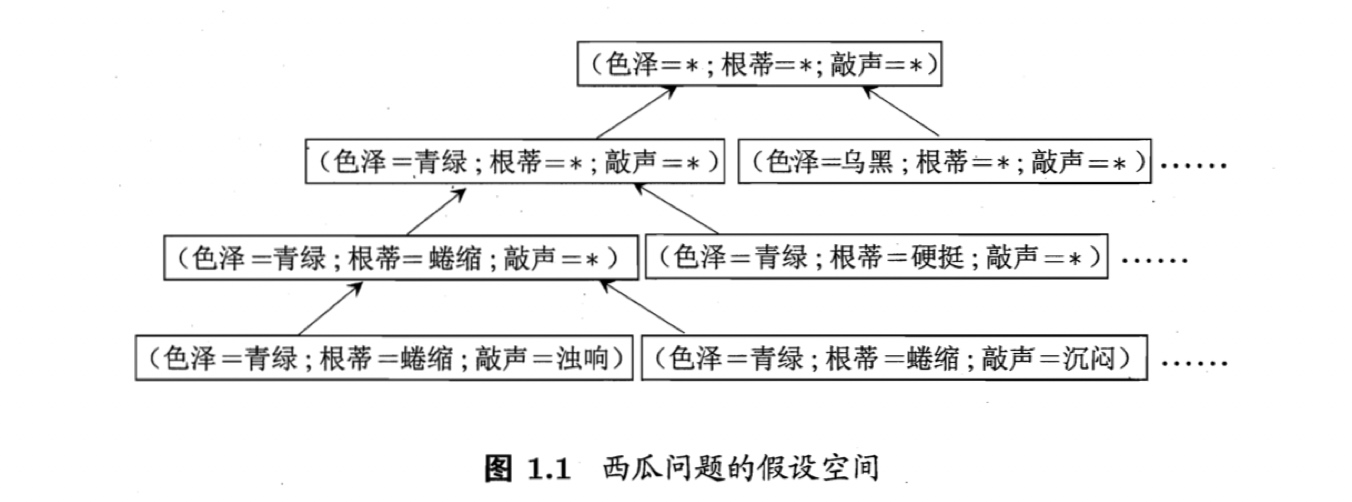
可以有许多策略对这个假设空间进行搜索,例如自顶向下、从一般到特殊,或者是自底向上、从特殊到一般,搜索过程中可以 不断删除与正例不一致的假设、和(或)与反例一致的假设。最终将会获得与训练集一致(即对所有训练样本能够进行正确判断)的假设 ,这就是我们学得的结果。
版本空间:与训练集一致的“假设集合”
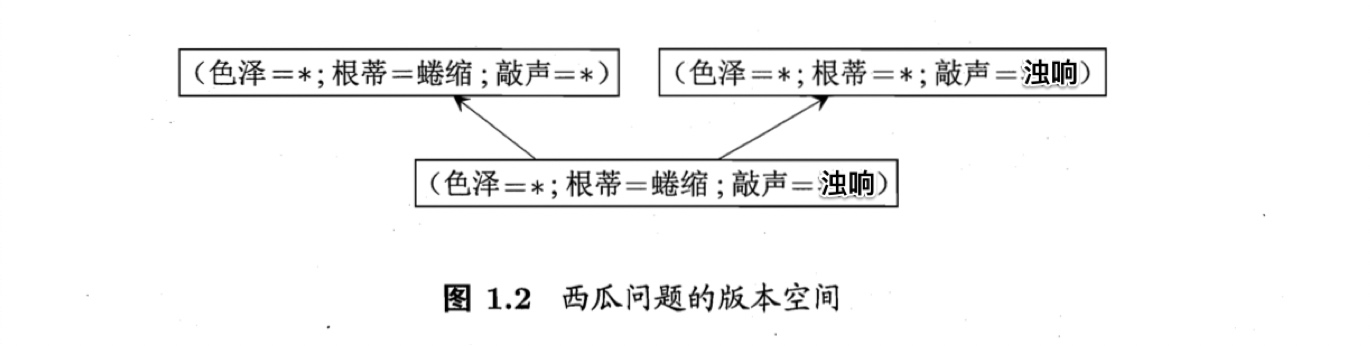
需要注意的是,现实问题中我们常面临很大的假设空间,但学习过程是基于有限样本训练集进行的,因此,可能有多个假设与训练集一致,即存在着一个与训练集一致的“假设集合”,称为“版本空间”(version space)。例如,在西瓜问题中,与表1.1训练集对应的版本空间如图1.2所示。
1.4 归纳偏好
若用学习到的三个假设(图1.2 西瓜问题的版本空间)来判断一个未知的西瓜是不是好瓜,可能会产生不同的结果。【有三个与训练集一致的假设,但与它们对应的模型在面临新样本的时候,却会产生不同的输出。】如,对一个新西瓜【样本】(色泽=青绿;根蒂=蜷缩;敲声=沉闷),采用左上假设->好瓜,右上->不是好瓜,下->不是好瓜。 “归纳偏好”就是要解决如上的问题,即面对一个新的样本,模型会输出一个确定的结果。任何有效的学习器必定有其“归纳偏好”,否则它将被假设空间中看似在训练集上“等效”的假设所迷惑,而无法产生确定的学习结果。
归纳偏好 inductive bias:机器学习算法在学习过程中对某种类型假设的偏好。
若模型偏好较“特殊”的假设,则会选择如左上、下;若偏好较“一般”的假设,则会选择如右上。
试用图形解释归纳偏好
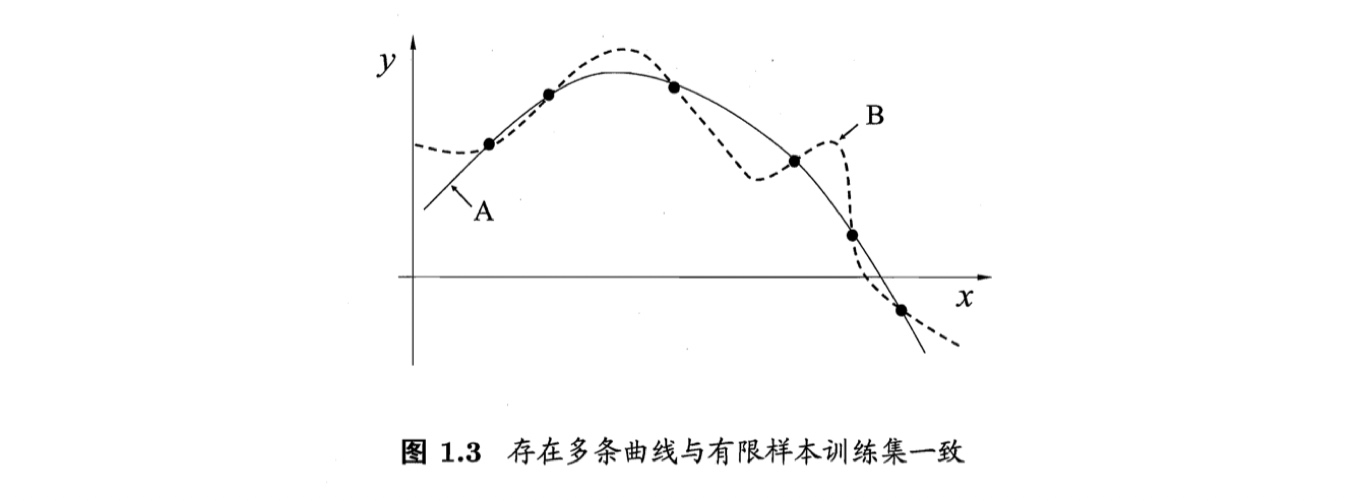
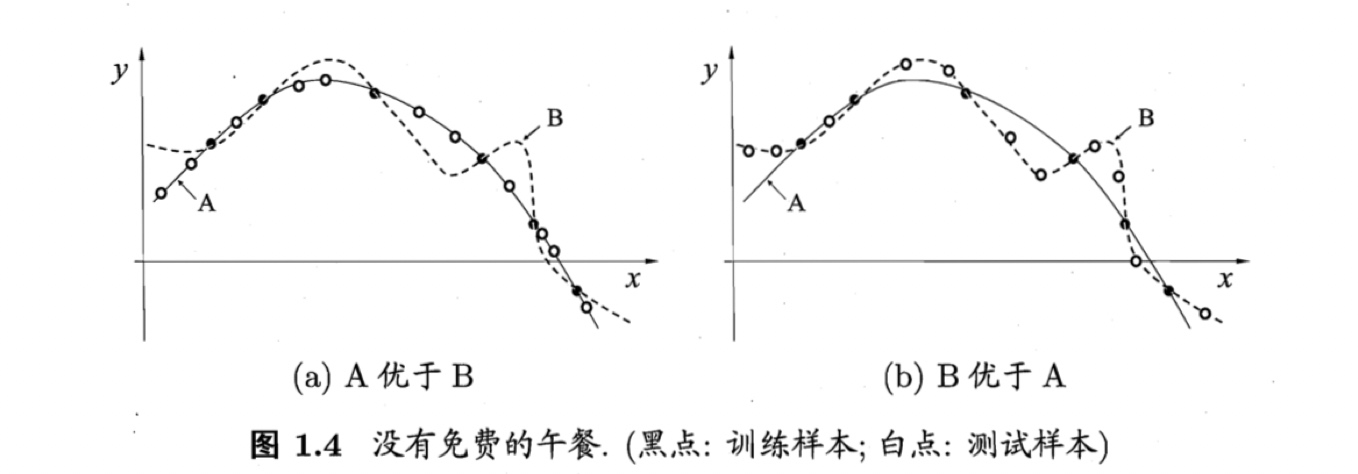
如果在二维平面坐标轴中,每一个点$(x, y)$都表示一个训练样本,要习得一个与训练集一致的模型,相当于在二维平面中找到一条穿过所有样本点的曲线。显然,能穿过所有样本点的曲线有无数条。若认为相似的样本应有相似的输出(如,在每种属性上相似的西瓜,成熟的程度应相当接近),则对应学习算法可能偏好图中较为“平滑”的A曲线而不是相对“崎岖”的B曲线。
奥卡姆剃刀原则 Occam’s Razor,什么是“好”模型?
归纳偏好可以看做学习算法自身在一个可能很庞大的假设空间中对假设进行选择的启发式或“价值观”。那么,有没有一般性原则来引导算法确立“正确的”偏好呢?“奥卡姆剃刀”(Occam’s Razor)是一种常用的、自然科学研究中最基本原则,即“若有多个假设与观察一致,则选最简单的那个”。如果采用此原则,同时我们认为“更平滑”意味着“更简单”,在图1.3中,我们自然就会偏好A曲线。 要注意的是,奥卡姆剃刀原则并没有指出“什么是最简单”,即对“简单”的不同定义会给予奥卡姆剃刀原则不同的诠释。如,上述对“好瓜”的三个假设,哪一个是最简单的呢?什么样的模型最好呢?
偏好与问题是否相配?“随机胡猜”不一定比“聪明”差
续上文假设,我们认为“平滑”A曲线更接近真实规律,如图1.4(a),A曲线的泛化能力优于B曲线。但实际情况也有可能是图(b)。换言之,对于一个学习算法a,若它在某些问题上比学习算法b好,则必然存在另一些问题,在那里b比a好。
“没有免费的午餐”定理 ( No Free Lunch Theorem, NFL 定理)
为了简单起见,假设样本空间$\chi$和假设空间$\mathcal{H}$都是离散的。令$P(h|X,\mathcal{E}_a)$代表算法$\mathcal{E}_a$基于训练$X$产生假设$h$的概率,再令$f$代表我们希望学习的真实目标函数。$\mathcal{E}_a$的“训练集外误差”,即$\mathcal{E}_a$在训练集之外的所有样本上的误差为
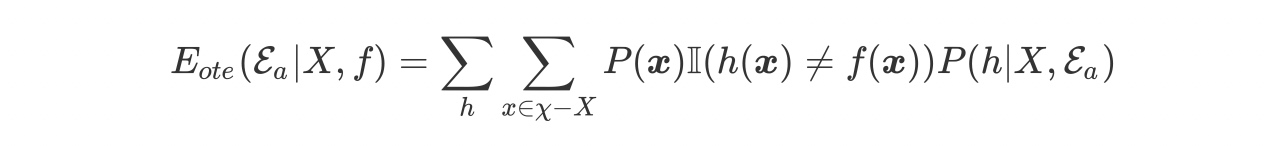
其中$\mathbb{I(\cdot)}$是指数函数,若$\cdot$为真则取值1,否则取值0.
考虑二分类问题,且真实目标函数可以是任何函数$\chi \mapsto {0,1}$,函数空间为${0,1}^{|\chi|}$。对所有可能的$f$按均匀分布对误差求和,有
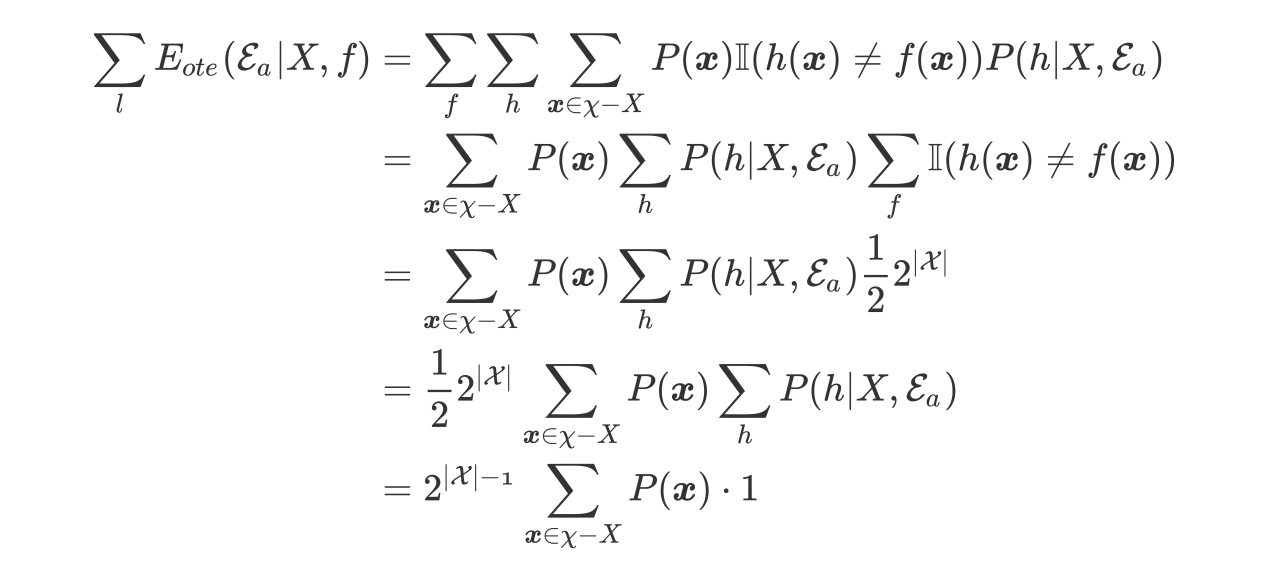
上式标明,总误差与学习算法无关!对于任意两个学习算法$\mathcal{E}_a$和$\mathcal{E}_b$,都有
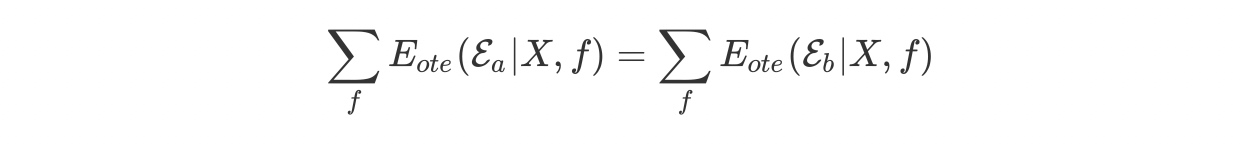
即,无论学习算法$\mathcal{E}_a$多聪明、学习算法$\mathcal{E}_b$多笨拙,它们的期望性能是相同的!这就是“没有免费的午餐定理”(No Free Lunch Theorem,简称NFL定理)[Wolpert, 1996; Wolpert and Macready, 1995].
NFL定理并不是想告诉我们“任何算法希望性能都相同”,它的寓意是“脱离具体问题,空泛谈论什么学习算法更好毫无意义”。(因为NFL定理有一个重要前提:所有“问题”出现的机会相等、或所有问题同等重要。但实际情形并非如此。)
1.5 发展历程
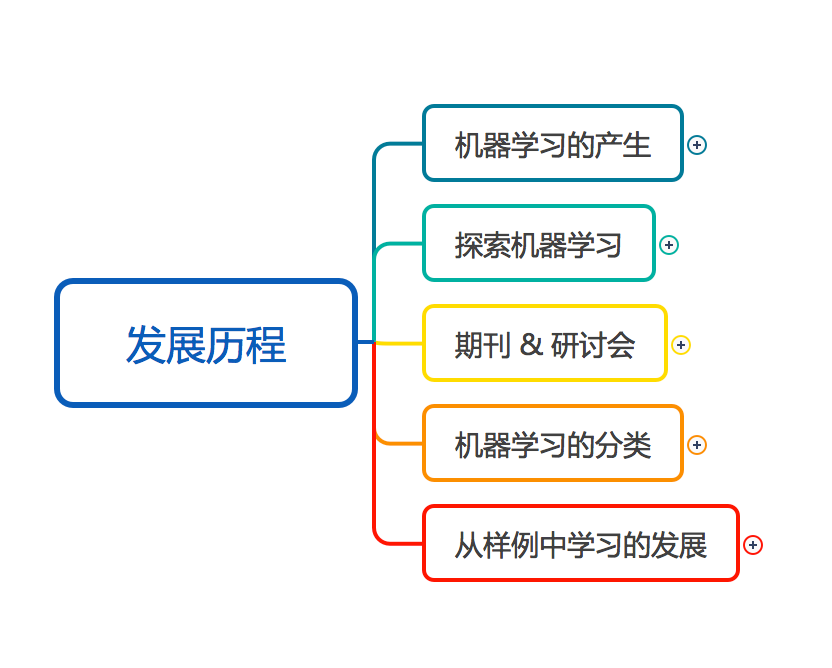

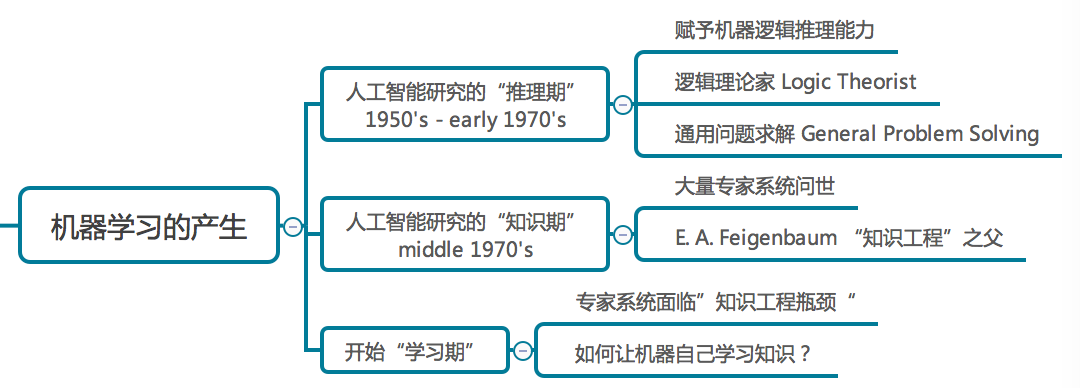
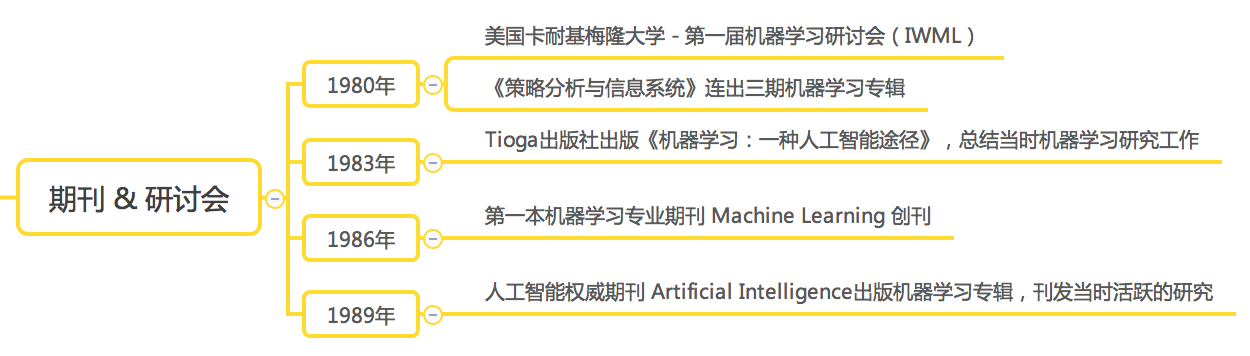
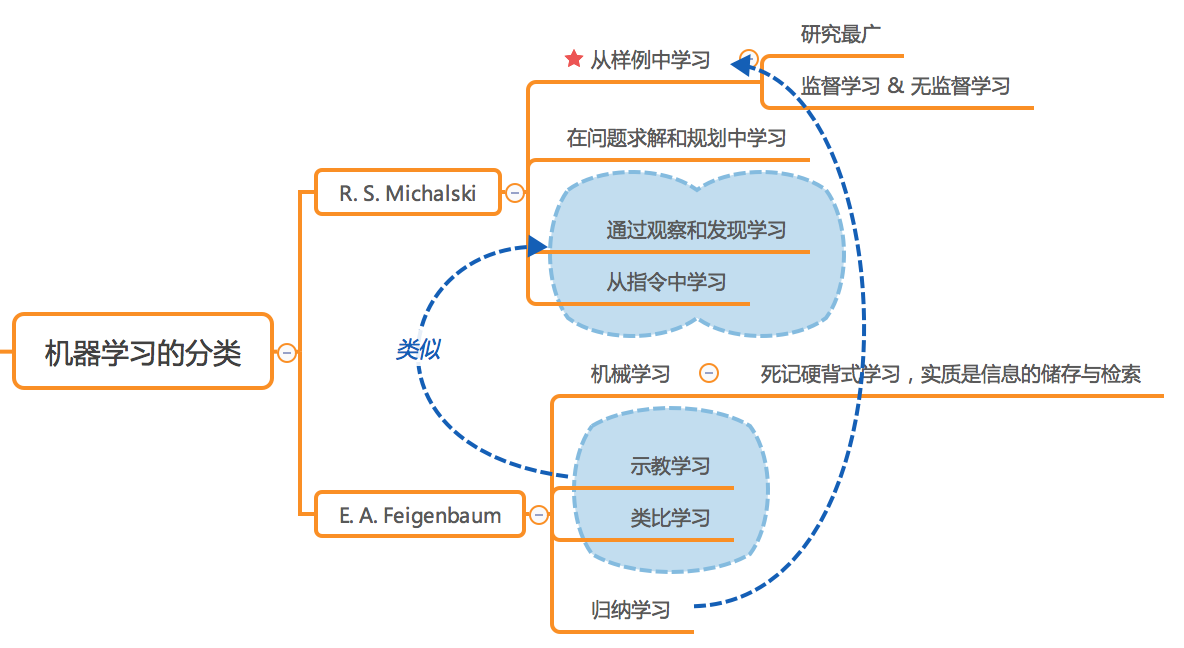

1.6 应用现状

Author Octemull
LastMod 2019-03-01